Andart

Random Roots

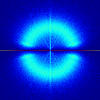
What is the distribution of roots of a polynomial with random coefficients? If you take a polynomial P(z)=a₀+a₁z+a₂z²+…+a_nzⁿ where the coefficients a_k are normally distributed random numbers and plot the density of roots in the complex plane you get the following interesting pictures.

This is for n=2,4 and 9. When n=99 everything is much sharper:

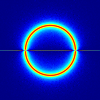
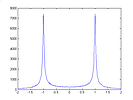
As the degree increases the roots tend to gather towards the unit circle, with another distribution along the real line. The fun part is that the circle seems to avoid the line, with a small cut-out in the distribution near –1 and +1. The distribution along the real line is two-peaked with sharp peaks:

The specialness of the real line is of course due to using real coefficients. They introduce mirror symmetry on the roots and make the real line special. If one uses complex coefficients only the ring remains (here n=9).

Like any other cool math idea somebody else has had it before me; when playing around with the problem I found several classic papers on the subject.

One of the first treatments was by Kac (1943), for real roots (explaining the two peaks). The trick for complex roots is to look at the correlation functions between polynomials and their derivatives (see also this brief presentation). This tells us that the density decreases as |Im(z)| as the real axis is approached, and that the density near the circle is proportional to 1/log|z| for large n. Apparently this holds even for non-independent coefficients

There are surprisingly many applications of random roots, both in pure mathematics, quantum physics and apparently antenna theory. See also the biography on random roots.

Plotting the density of roots of polynomials with integer coefficients produces other nice pictures. I looked at polynomials with –1,0 or 1 as coefficients.

As the degree increases they converge to the usual circle plus real line. But for intermediary values a beautiful pattern appears: isolated “castle” roots surrounded by moats, forming what looks like a fractal pattern. Actually, for any finite degree the distribution is just a lot of Dirac delta functions since the number of polynomials that can occur are finite (but growing exponentially with degree).

In what order is the holes filled out? Here I let the color correspond to the lowest degree equation that produces the root, with red for n=2 and the darkest blue (beside the background) for n=11. The higher degree roots distribute themselves between the already existing roots, slowly approaching them. Note that the probability density and degree seem related: low degree roots are much more common than high degree roots.

Another natural (?) distribution of the coefficients is the uniform distribution on the Poincare sphere. The result is a broad ring with a spike at zero; the complex coefficients of course makes it rotation symmetric.

A more odd distribution occurs if we use the same distribution for real coefficients; they will be Cauchy distributed along the real line. The result is of course a lot of roots long the real line (this time just one peak), but the ring turns into aurora-like crescents. Streaks with higehr density seem to approach the origin along different directions. Plotting the density of roots with different arguments shows clear peaks and maybe notches around them:

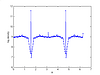
I'm not sure why they appear.

On the Cusp of a Great Novel

Cusp by Robert A. Metzger starts with a bang - the sudden appearance of megascale structures on Earth nearly wrecking the biosphere, artificial superflares on the sun that threaten to move it and a net-based superintelligence on the loose. That, enough stuff to act as a climax of an ordinary sf novel, is all in the first chapter of Cusp.

It actually manages to beat the prologue with its finale.

The strength of this novel is the sheer number of enormous ideas thrown together. Like colliding continental plates they produce quakes and mountain ranges; the result is a rugged landscape of wild possibilities and abysses. A bit like how The Authority took the superhero drama and added the millions or billions of innocent bystanders that get squashed when the titans fight. Cusp is refereshingly upfront about the ecological and human consequences of attempting to move a planet.

OK, enough geological metaphors (and I will resist any pun on 'earth-shattering'). Let's just say that any fan of Greg Bear's planet-smashing (The Forge of God, Anvil of Stars) will like the novel.

The downside to all this is that megascale drama tends to make human characters rather puny unless they are equally megascale posthuman. And while there certainly are a few posthumans around, they and their characterisations are not of the same order of magnitude as the concepts. The villains (if they can be called that) are somewhat stereotypal in style and motivations, although the interplay between different agendas, determinism and free will, does produce a nice mess.

There is also the problem that while many big ideas are thrown together, not all of them are new. In fact, many of the big concepts have been used before, and here appear in a grand melange. This can produce a hopeless mess (Howard Hendrix's Standing Wave comes to mind), but Cusp actually manages to put it all into a reasonably coherent pattern.

The big success of Cusp is probably that it manages to twist expectations so often. Throughout the middle of the novel there is on average one, expectation-changing revelation per chapter. That is far better than most novels manage in their entire plot.

Hermetic kitsch

Today I couldn't resist raytracing the image to the right, a rendition of the tree of life of the kabbalah.

I have a somewhat mixed relationship to hermeticism. On one hand I'm a firm materialist/monist, with a sceptical mindset and nothing but scorn for wishful 'magical' thinking. On the other hand I enjoy hermetic symbolism and its ties to the most unexpected areas of western thought, as well as the interesting potential of using symbols and belief to program one's subconscious. Sure, it can be done using more 'clean' psychological methods, but it is more fun (and greater psychological impact) to use complex old symbols with the weight of tradition. It is a bit like kitsch: it is embarrasing, gaudy, tells us a lot about our culture and - admit it - fun.

Beside my more practical objections to hermeticism (i.e. that I don't believe in the underlying metaphysics and think it has a feudal family-normative subtext) I have en epistemological problem with much of the school. It is too arbitrary. Most of the symbolic sets used (the zodiac, the ten sephiroth, the four elements etc) are arbitrary assemblies that are then elaborately rationalised. Much hermetic thought is devoted to elaborating the correspondences between such sets and explaining away apparent contradictions like why aquarius is an air sign.

Take any set or sequence of images, especially concepts and images that can be interpreted openly, and you can with relative ease develop a consistent explanation for why they have to hang together or why image 2 follows image 1. It is the same principle Scott McCloud demonstrates in chapter 3 of Understanding Comics (In my opinion a great book about cognitive psychology), or for that matter the "what the thinker thinks, the prover proves" from Robert Anton Wilson's Prometheus Rising.

I ran into this phenomenon when I wrote a small text about 3D generalisations of lineal figures (pentagrams, hexagrams, etc) to the symmetries of regular polyhedra and it was well received in the online esoteric community. But I realized from the start that my scheme was largely arbitrary: it would be trivial for someone else to factor the symmetry groups in other ways, creating totally different correspondences and meanings. But nobody came forth with a rival scheme. Clearly it was enough to just claim a set of correspondences. That hermetic thinking tends towards accepting authority is one thing, but given that it also claims a kind of pythagorean mathematical internal consistency correspondences should not be under-constrained. Yet this is the case for many esoteric concepts, be they gematria or the tree of life.

The tree of life originates in the Sefer Yetsirah (3-6th century AD) although it can probably be traced to older Hekhaloth mysticism. The basic idea is a fairly neoplatonist account of how creation occured, with different emanations or functions of God manifesting in sequence producing the ten sephiroth. In Sefer Yetsirah the motivation of the number ten appears to be both the number of fingers and the six directions in space, two in time and two "moral" directions. This is loose enough, but the real mess occurs when these ten are linked by 22 paths corresponding to the letters of the hebrew alphabet (the linkage is not that strange, since the letters were also seen as having numerical qualities). The Sefer Yetsirah uses a 3D arrangement of the sephiroth, while the modern tree is a 2D graph (this link is also a good example of the fun geometric/combinatorial games one can play in hermetic thinking). There have been many different arrangements of the 22 paths and the resulting graph, but today just one of the 3 190 187 286 possibilities is in use (and a few different attributions of which letter to which edge). While one can certainly limit the possibilities by requiring certain symmetries it still seems rather underconstrained (especially by the short descriptions in the Sefer Yetsirah). The current arrangement appears to have been crystalised around the early 1600's, as seen in Robert Fludd's widely reproduced image, perhaps even as early as the 13th century in the Sefer Zohar. There have been some ideas of extending the tree into a 3D structure (cf. Israel Regardie's The Complete Golden Dawn System of Magic), but these mainly multiply the sephiroth while leaving the underlying graph largely unchanged.

Perhaps the best and most no-nonsense approach to deriving the tree is Colin Low's Notes on Kabbalah (chapter 1) that actually makes a fairly plausible sounding argument for the arrangement. I still find the paths rather arbitrary, though.

One can of course imagine a die hard hermeticist claiming that the numbers 10 and 22 are constraints (presumably given by deeper origins), and choosing a particular set of paths constitutes a case of symmetry breaking - God is forced to make a contingent decision resulting in a particular kind of universe out of a larger set of possibilities. Maybe our hypothetical hermeticist then runs off to do an argument based on the anthropic principle showing why just beings living in this kind of universe would be conscious of the situation, and so on. Might make a fun paper for Journal of Quantum Kabbalah C (Cosmogony). But it doesn't convince me much.

In the end it seems more reasonable to accept that the tree is a very human creation with particular cultural origins - Hekhaloth mysticism combined with gnosticism and early numerological/combinatorial speculations, medieval exegetics, renaissance memory arts, victorian masonic symbolism and syncretism. It is a relatively simple graph to hang mountains of associations and speculations on. Not to mention to visualise covered with as much hermetic kitsch as one cares.

After all, when one adds too much stuff to any art it becomes kitsch. Already the color associations of the sephiroth (in any of the four different systems!) makes the sober graph a bit kitschy. By the time Fludd is finished with it we have holy names, cherubs, emanations and the tablets of Moses. Maybe that is one of the important hermetic secrets: esoteric symbolism provides enough gravitas to allow us to enjoy kitsch without guilt. It is a cultural counterweight to the pink flamingos of loose thinking.

To get back to my own image (and its pink flamingos), it does have a few fun features. I made the tree using metaballs hovering above a mirror, producing the internal tree. One is of course welcome to view this as the "opposite" or qlippothic tree, but the most delightful effect is the small inverted trees refracted through the sephiroth. Not unlike the nested trees that sometimes crop up in discussions of the four worlds, but this time suggesting that every sephira contains a small qlippothic tree. Maybe my image is just generally heretic.

The Bad Habit of Addictification

Today I attended the release of Eudoxa: Eudoxa Repoer #6: Fair Play och moralpaniken by Rasmus Fleischer, a report dealing with the issues of moral panic, gaming, internet addiction and how NGOs work to become part of the government. Unfortunately right now only available in Swedish, but I'd like to summarize a few interesting points.

The background is the organisation Fair Play and their media-successful claims that computer games increase violence and are addictive. In fact, many forms of computer-use are apparently addictive according to Fair Play.

The first point of the report is to question this addiction account. Is there addiction (or dependency) on computer games, and if it exists, is it necessarily bad?

Addiction can be defined as a craving for something that develops into a dependency and continues even thought it is causing the addicted person physical, psychological or social harm.

Often the term is used for the brain disorder that causes loss of control of drug-taking behavior: quite a few people use drugs or other things without being addicted. However, recognition of this modern vulnerability view has been slow in coming to Sweden, partially through the opposing "addiction as a exposure-induced epidemic"-view forcefully promoted by Swedish drug-control pioneer Nils Bejroth (Rasmus also makes the case in the report that there is a direct descent of ideas from Bejroth to Fair Play). In any case, I will use the first definition for the rest of this entry.

The widely accepted definition of addiction as craving something harmful clearly makes anything addictive harmful - it is not possible by this definition to be addicted to something neutral or good. Hence addictive becomes a powerful rhetoric attack on anything seen as undesirable. It is enough to show that it produces (or that it might produce) cravings for more or dependency, and it instantly becomes something dangerous.

However, dependency is not necessarily dangerous. We are all dependent on air and water. Less trivially, most of us have a shoe dependency: we cannot walk outside well without good footwear, since we have used it since we learned to walk. This dependency, like all dependencies, limits our range of actions. But it actually increases the range in other directions - Swedish winter is not survivable barefoot. A drug dependency can be entirely manageable if the drug is cheap, safe and plentiful - such as caffeine - or if the benefits given are greater than the costs - as in the case of many chronic medications. One aspect of gaming Fair Play does not seem to stress is whether gaming or computer use could have beneficial aspects.

Cravings are also not necessarily negative, not even when they are self-reinforcing. In the video "Dödligt Spel" ("Deadly Game") shown in the schools by Fair Play, cognitive neuroscientist Martin Ingvar points out that games are designed to be both easy enough to play, but constantly challenging in order to both reward us, draw our attention and force us to give our outmost. In the surrounding context that sounds quite sinister. Add to this that time seems to vanish during the game. But this is also almost exactly the definition of Flow from Mihalyi Csikszentmihalyi! In Flow: The Psychology of Optimal Experience Csikszentmihalyi argues that this kind of skilled focus is a key component in growing as a human. Taken in the context of humanistic psychology, flow is seen as something desirable and important for humans to develop. And games, like any other activity, can be the focus. Rather than claiming that self-reinforcing focus necessarily leads to harm, this view takes the more open view that it can also produce positive effects. It remains to be demonstrated that a certain self-reinforcing activity is more likely to be harmful than helpful, if one wants to make the case that it is addictive.

Overall, it has become fashionable to addictify nearly any human activity. We are sex-addicts, shopaholics, tv-addicts, roleplaying addicts and junk food addicts. It removes responsibility from the "addict" (since he clearly no longer holds full responsibility for his actions) and from the close social network (since it was the addicting properties of the object rather than any of their actions or inactions that caused the addiction). Outside helping institutions get a raison d'etre and money to act, creating a public choice incentive to expand - and make more people aware of the dangers of their particular kind of addiction.

The 10-question test of whether you are a "screen addict" is taken nearly point by point from DSM-IV's checklist for substance abuse disorder. But by separating out mild effects such as "thinking about the Internet when not connected" or "being irritated when not able to get connectivity" from heavy issues such as "committing crimes to sustain the computer use" makes it far more likely that people will get high scores and hence be diagnosed as addicted. Directly mapping drug abuse criteria to another domain can seriously reduce validity (taking heroin each day is a severe addiction, but playing a game each day?). An interesting exercise is to replace "computer" and "net" by "books" and "libraries": clearly most of my academic friends suffer from severe cases of text addiction.

But books and writing are held in high esteem in our culture. We might smile at the reclusive bookworm or the driven author, but few would consider sending them for psychiatric treatment curing them of their love with text. But computer games are the lowest of the low (OK, maybe pornography manages to get in below them) of our media, at least seen from an upper middle class perspective rooted in traditional art and culture. They are commercial, american, violent, engaging and involve technology. Rasmus makes another interesting connection when he points out the links between people involved in Fair Play and the traditional art/culture establishment, and strongly argues that the artistic and cultural merits of computer games are being ignored.

If games and computer use do not have any redeeming qualities, then their ability to start craving-loops or dependency would imply that they are addictive and negative (but again, the level of addiction and negativity would require an empirical study). But if one accepts the view that at least some computer activities indeed are positive, then the issue becomes far more complex. Then it is not just an issue of reducing child computer usage (Fair Play promotes bribing children to have computer-free days) but to find ways of encouraging the positive activities. As Rasmus points out, learning the skills required for an IT world is best done intensively and from an early age. I know I would never have gotten a Ph.D. if I had not started by spending hours and hours as a kid before my Sinclair ZX81 doing simple simulations and games. A majority of online gamers cite social contact as a key point in the game, something that deflates the Fair Play claim that computer games tend to desocialise people. Many games do stimulate imagination, visuomotor skills, strategic thinking or at least reading English.

Perhaps the first step to get out of the either-or trap of imaging computers and games as either addictive and negative or neutral and non-addicting, is to refrain from using the term addiction. Addiction is deep down a case of mislearned habits. And by allowing ourselves to use the far less loaded term "bad habits" it becomes much more manageable to discuss the problems of misuse of computer games. Games and computer use can cause bad habits. In a few cases these bad habits are so severe that they could be viewed as an addiction (again, likely due to a vulnerability to addiction formation), but the vast majority of users with bad computer habits merely stay there. There is no evidence that people who game a bit too much end up in a downward spiral towards violent computer-junkiedom. In most cases the bad habits clear up sooner or later, due to individual decisions (I once erased Sid Meier's Alpha Centauri to get work done) or interactions with family or friends. Viewing the problem as one of regulating habits rather than invoking the entire pantheon of addiction puts the control in the hands of the people involved, not among outside groups.

A Doll's Madhouse

Die Anstalt - Psychiatrie für misshandelte Kuscheltiere is probably the most unusual flash game I have ever encountered. You take on the role as a psychiatrist trying to cure traumatized dolls.

The game both parodies psychiatry and makes some aspects accessible. It manages to be both humorous and sometimes unnerving - the dolls have serious troubles, the therapy can backfire and one cannot help empathising with them. I felt relief and joy when I finally managed to cure Dolly the sheep.

Of course, that is what dolls are for, whether real or virtual: they represent ourselves in a highly abstracted manner. The game would likely not have been very successful with virtual people in treatment: either it would have become a medical The Sims game, or far too creepy to really work as a game. Having dolls act our self-destructive impulses or psychoses strikes a balance between identification and distance.

The player is present in the game only as his arm, stretching into the picture to play with the dolls or give them things. This manages to connect the player to the scene. Had it just been a case of pressing icons, the player would have taken the role as some omniscient, omnipresent psychiatric god. Had the arm been attached to a character on the screen, the player would just have been directing that character, not been present in the therapy.