Andart

Dirty math

Some time ago I posted a steamy dodecahedron picture. Generally erotic mathematics is under-represented on the net (despite, or perhaps because, sex is sublimated mathematics urge). However, thanks to Boing Boing I encountered the pictures by Mirko Ilic, Sex and Lies Part I and II. Here we see the disturbingly erotic potential of cylinders, lemniscates and various manifolds.

While looking for my original post I discovered http://nakedgeometry.com/. This goes the other way around, eroticising various geometrical shapes by building them out of humans. The images are not that risqué; the shapes of Ilic are far more sexual. Even if the characters were engaged in sexual activity I doubt they would reach the same intensity as the abstracted fleshiness of the nonhuman shapes - there is a focus and ambiguity there that is lacking in the more architectonically elaborate but far too transparent structures. Real sexuality might require a certain murkiness, even when it is mathematical.

(Obligatory, and NSFW, Oglaf reference - I wonder how common polyhedral fetishism is?)

Why I don't trust Hubbert peak arguments

Recently a post on the Extropians mailing list pointed me to Ugo Bardi's essay "Entropy, peak oil, and Stoic philosophy". Oil, curve fitting, doom and philosophy. What is there not to like?

Lots of data points fitting the curves: good evidence for future predictions, right? Not so fast. It turns out that even something as well behaved as a Gaussian-like curve becomes an unruly beast when trying to fit it with incomplete data.

The basic problem is this: all the lovely curve fits are done to past data where we have the whole sequence from a slow start, exponential increase, peak and then exponential decay. Fitting a curve to a complete data set is very different from fitting it to data that is still arriving: retrodiction is *far* easier than prediction.

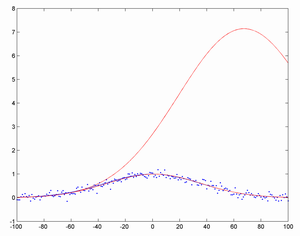
Here is a simple example. I start by taking a Gaussian curve centred on year 0 with a standard deviation of 50 years, with added Gaussian noise of standard deviation 0.1 (i.e. about 10% of the amplitude of the big curve). Then I try fitting a Gaussian to the first N points, and see how well it manages to predict where the peak will be.

The results are pretty bad. At first the fits are all over the place, driven purely by noise. As time goes on, they merely become bad: if you see a roughly exponential increase if is very hard to tell when it is going to stop (the high red curve is based on the first 25% of the data). Eventually, when you have reached the peak (lower red, based on 50% of data), they snap into the right shape and approach the true curve (blue).

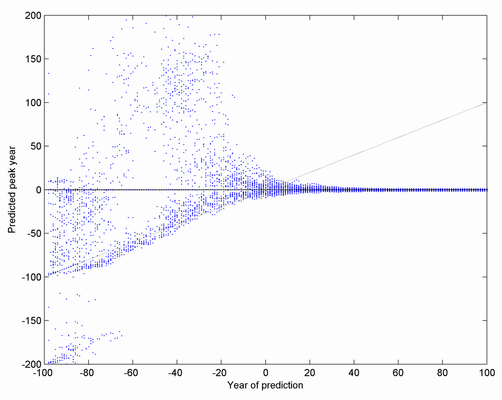
Here is another way of visualizing the results. I plot the predicted peak (y-axis) versus the time the prediction was made (x-axis), for 50 realizations of the noise. As you can see, the predictions are quite worthless until very close to the peak. Afterwards they are just fine, of course. There is also a preponderance in the early days of predictions that the peak is already upon us (the cloud along the diagonal line).

Note that this is an ideal case where the noise is not overwhelming (the problem persists even when I use one tenth as strong noise), the type of curve I am trying to fit actually is the same one as the true one and we have lots of data points with no bias. Reality tends to be worse. Just consider how much selection bias can be introduced by unconsciously picking the right datasets that fit one's theory and discarding the others as 'biased' (especially since you can get nearly any peak by choosing different end dates of your time series). We tend to be overconfident in our ability to predict and remain unbiased.

What to do? The first thing is to stop relying on extrapolated Hubbert peaks as arguments for that we have reached peak oil about now. We can only trust the curve fit if some *other* line of reasoning makes us think we are indeed near or after the peak. Arguments based on other methods are very important - there are plenty of geology, economics, technology and other disciplines that can be brought to bear on the question. In fact, the more *different* lines of evidence are brought to bear on an issue the more reliable the conclusions will be. Past data should feed into rational Bayesian estimation of the real state of the world, but it can be much less powerful than it seems at first glance.

Nice looking retrodictions are not good evidence that predictions will be equally good.

(Edit the 26th May to make conclusions clearer)

Premiere

If you are around Amsterdam on June 26 (and have an invitation) you might want to see the premier of the film "Transhuman" at at 14:15 in the Nieuwe DeLaMar Theater. Well, at least *I* want to see it, since it is a documentary about transhumanism that includes me a lot :-)

You can see some pictures here, including the wonderful image of me reading all the books at Blackwell's bookstore in parallel.

Minireport on planetary defense on IEET

James Hughes updated a minireport I whipped up on the planetary defence conference into Progress in Mitigating Asteroid Impact Risks. Thanks!

I will try to put up a blog version of my talk later,but this weekend I have the Humanity+ @ Parson to think about. Ah, the jet-set academic lifestyle... and oh the accompanying jet-lag! :-)

In the meantime, enjoy this map of the asteroid belt and trojans. It is a crowded place.

Playing with asteroids

I have had great fun with the Asteroid Orbital Elements Database. Here is a plot of the main belt and Trojans:

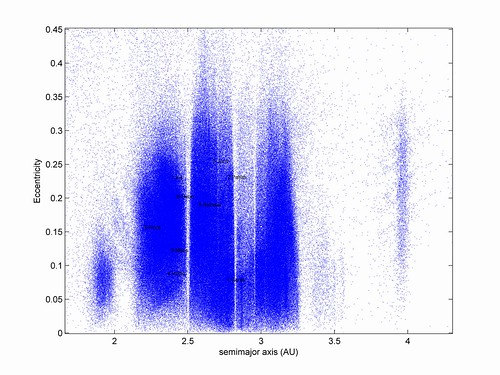
Plotting the size of the orbit and eccentricity shows the various asteroid families and gaps due to gravitational resonances:

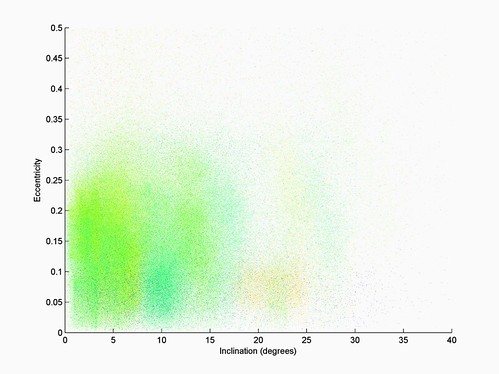
There are families in terms of inclination too, of course. Plotting inclination vs eccentricity with distance as color gives this image:

Probabilistic heroism: how road inspectors and planetary defense are alike

I am attending the 2011 IAA Planetary Defense conference. A.C. Charania has a planetary defense blog with plenty of interesting material.

Some ponderings amid the mission planning diagrams, impact-porosity discussions, asteroid statistics and nuclear detonations:

Someone who saves a life is a hero. I don't care about whether this is done at personal risk or not; it is the altruist consequence that matters.

What about somebody who saves a life probabilistically? Imagine seeing a rock poised above a busy road: it might fall, leading to a landslide killing several people. I would argue that you are just as much a hero if you roll the rock back and prevent it from ever falling as if you were to jump in just when the rock was already falling (or somehow shielding the victims from the landslide). Where in the causal process you intervene doesn't matter, except that the uncertainties increase (so you might become a tenth of a hero if you remove the risk of one death with probability 10%)

Now, what about checking unsafe rocks above roads? There are many rocks, some might be dangerous, but most are safe. But if we do not do anything we should expect that there could be a sizeable risk - our a priori estimate of the fall probability implies a non-zero expected number of harmed people. As we investigate the rocks we might find that none are unsafe. The risk has become zero. I think this should also be regarded as a probabilistic heroic action.

Sure, nobody was ever in risk in this case, but we did not know that. One can distinguish between objective probability (the "actual" probability in the world) and subjective probability (a Bayesian view, where probability denotes our state of knowledge of the world). The objective probability was never affected, but we cannot base our actions on objective probabilities since we do not know them - as rational beings we can at best act according to our subjective probabilities.

It is a bit similar to the legal hair-splitting about incompetent murderers. Suppose you try to kill somebody, stupidly thinking that sugar is a deadly poison, so you spike his food with sugar from a jar. In this case (I have been told), the Swedish legal system would not consider it attempted murder since there was no way it could have succeeded, despite the ill intention. If you instead try to use rat poison but the mislabelled jar contains sugar, then it is attempted murder - it was just averted due to dumb luck. The expected number of victims would have been close to one.

So by this line of argumentation, checking the rocks with the intention of trying to fix the dangerous ones is heroic. It might be heroic because you find a rock you fix, reducing the objective risk, or because you find that all rocks are safe, reducing the subjective risk. The end result is the same: a safe road.

I think we can make an analogy from this to stopping asteroids. Thanks to current surveys we know around 90% of all near Earth asteroids large enough to cause massive disaster if they were to hit. None of them are dangerous over the next century. A bit more surveying and we will be able to completely retire this risk (there will be some remaining risk from long periodic comets and non-global risks from smaller asteroids, of course). Before this started there was an unknown risk, bounded only by historical evidence (biased by observer selection effects). Today the risk estimate is on the order of a few thousand expected dead per year, mostly due to very rare but deadly large impactors. This risk is falling fast as more and more are surveyed.

So in this slightly quirky way the people around me at the conference are saving thousands of lives per year just by checking what is out there. It is not the active heroism of actually rushing out there and deflecting a NEO or stopping a falling rock, but the discreet and large scale probabilistic heroism of keeping roads safe.

By this line of argument I am sitting among a whole bunch of impressive heroes.

Hear me uncut

An interview with me from the Canadian radio program Spark: Full Interview: Anders Sandberg on Whole Brain Emulation.

Partitioning the sphere

Recently, while working on an application, I encountered the problem of picking points 'evenly' on a sphere. This is a classic, slightly ill-posed problem (what is the goodness metric?) Putting a spherical coordinate grid is a bad idea, since it will be dense near the poles. Uniform random distribution of points (by normalizing 3 normally distributed random numbers) will have pairs close to each other. The Thomson Problem phrases it in terms of electric repulsion between points constrained to the surface, and suggests an obvious energy-minimization particle method. Katanforoush and Shahshahani (pdf) has a nice review discussing several methods.

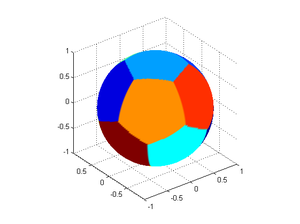
Since I have been playing with centroidal Voronoi partitions I wondered if they work for sphere point distribution. So I implemented a Matlab script that takes N points, puts them on a sphere, calculates what points on the sphere are closest to each point, moves the point to the centre of the region, and repeats until a certain tolerance is met. A complication is that I use a bitmap method, giving me more pixels near the poles, so I also reduce the weight of polar pixels.

Here is the script: CVPsphere.m

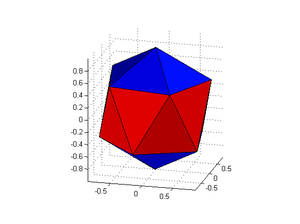
The result is pretty neat. For 12 points they distribute themselves so they produce 12 spherical pentagons, with a convex hull of the points forming a nice icosahedron. However, the distribution is not perfect: colouring the faces by their area shows that the equatorial faces are slightly bigger than the polar cap faces.

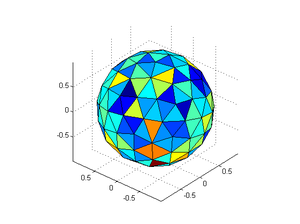
Still, the distribution is slightly uneven. There are a few too many 5- and 7- corners. So I also did a force-directed layout, using the Thomson problem approach: forceSphere.m

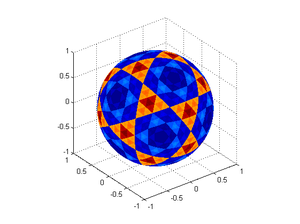
Another approach is subdividing triangles, starting from an icosahedron. I did a simple (simplistic?) implementation using convex hulls rather than do the cumbersome tracking of triangles. Here is the code: geodesicSphere.m

It is less flexible than the above methods since you cannot control the number of points, but it is much more geometrically smooth. It is worth noting that the areas of the triangles are not perfectly identical, and forms a nice recursive pattern:

OK, which method is best? I guess that depends on what you care about. I can think of two metrics: the evenness of the areas and triangles of the convex hull and the minimal distance of neighbours. So here is a comparison:

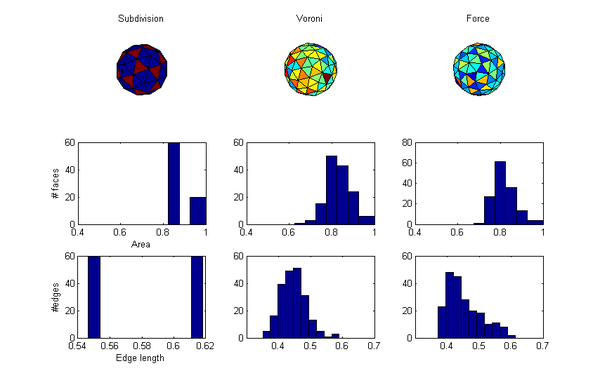
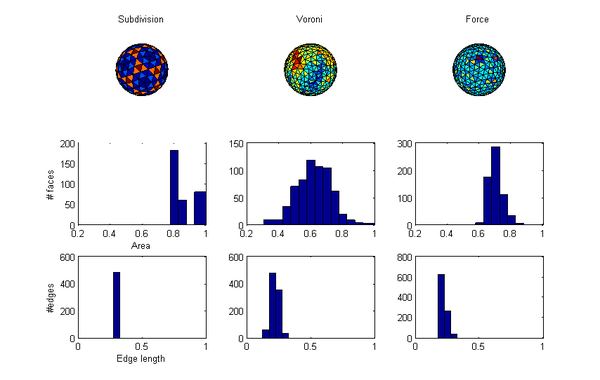
So, the Voronoi approach doesn't come out that well. Broad area distribution and edge lengths (about as bad as the force approach). While tweaking can likely improve things, the geodetic division also has computational advantages (if implemented right). The main downside of the geodetic approach (and to some degree the Voronoi approach) is the systematic distribution of areas, which in some applications is problematic. Still, it is a fun exercise to write the code.