May 10, 2011
Partitioning the sphere
Recently, while working on an application, I encountered the problem of picking points 'evenly' on a sphere. This is a classic, slightly ill-posed problem (what is the goodness metric?) Putting a spherical coordinate grid is a bad idea, since it will be dense near the poles. Uniform random distribution of points (by normalizing 3 normally distributed random numbers) will have pairs close to each other. The Thomson Problem phrases it in terms of electric repulsion between points constrained to the surface, and suggests an obvious energy-minimization particle method. Katanforoush and Shahshahani (pdf) has a nice review discussing several methods.
Since I have been playing with centroidal Voronoi partitions I wondered if they work for sphere point distribution. So I implemented a Matlab script that takes N points, puts them on a sphere, calculates what points on the sphere are closest to each point, moves the point to the centre of the region, and repeats until a certain tolerance is met. A complication is that I use a bitmap method, giving me more pixels near the poles, so I also reduce the weight of polar pixels.
Here is the script: CVPsphere.m
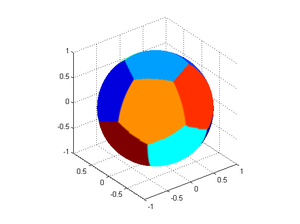
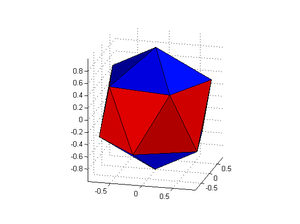
The result is pretty neat. For 12 points they distribute themselves so they produce 12 spherical pentagons, with a convex hull of the points forming a nice icosahedron. However, the distribution is not perfect: colouring the faces by their area shows that the equatorial faces are slightly bigger than the polar cap faces.
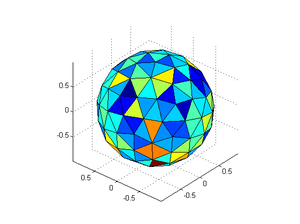
Still, the distribution is slightly uneven. There are a few too many 5- and 7- corners. So I also did a force-directed layout, using the Thomson problem approach: forceSphere.m
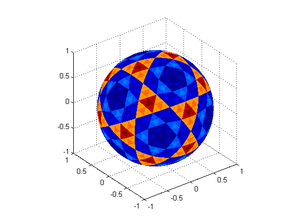
Another approach is subdividing triangles, starting from an icosahedron. I did a simple (simplistic?) implementation using convex hulls rather than do the cumbersome tracking of triangles. Here is the code: geodesicSphere.m
It is less flexible than the above methods since you cannot control the number of points, but it is much more geometrically smooth. It is worth noting that the areas of the triangles are not perfectly identical, and forms a nice recursive pattern:
OK, which method is best? I guess that depends on what you care about. I can think of two metrics: the evenness of the areas and triangles of the convex hull and the minimal distance of neighbours. So here is a comparison:
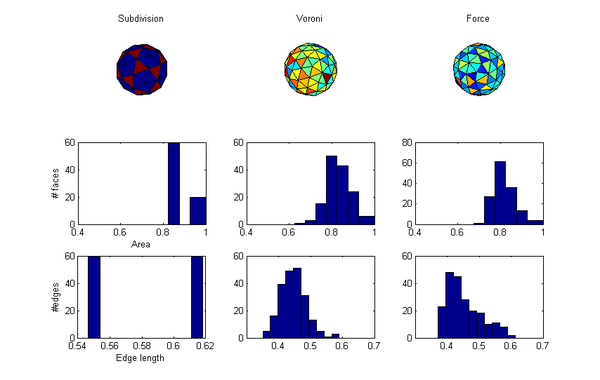
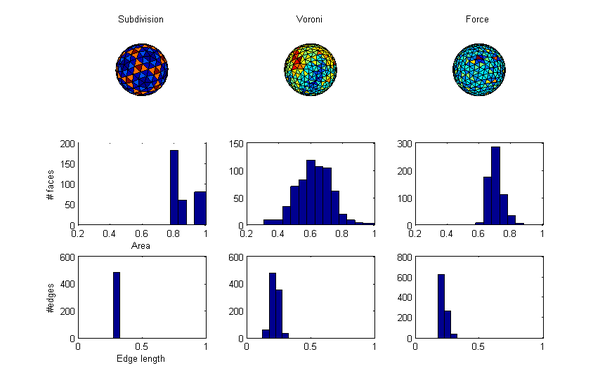
So, the Voronoi approach doesn't come out that well. Broad area distribution and edge lengths (about as bad as the force approach). While tweaking can likely improve things, the geodetic division also has computational advantages (if implemented right). The main downside of the geodetic approach (and to some degree the Voronoi approach) is the systematic distribution of areas, which in some applications is problematic. Still, it is a fun exercise to write the code.
Posted by Anders3 at May 10, 2011 09:41 AM