August 28, 2010
The wikiBerry paradox
The interesting number paradox pretends to show that there is no smallest uninteresting number (because otherwise it would be interesting for this reason).
Yesterday one of my friends (I think it was Stuart) suggested the Wikipedia version: the smallest integer without a page in Wikipedia. A quick check suggests the smallest integer without its own page (at the point of writing) is 217. Given this important property, clearly it deserves its own page (and if it got it does not deserve it, and so on).
Of course, Wikipedia has an easy way out: declare that the whole issue is not notable. This is similar to declaring that all numbers and their properties are uninteresting. Declaring it not notable works unless it becomes a big debate like malamanteau (214,000 hits according to Google right now). Overall, XKCD has amply demonstrated that like complex formal systems powerful enough to allow self-reference Wikipedia has Gödel-like topics it cannot cover according to its own rules. Of course, not being a formal system and run by intelligent agents the attempts of getting out of such states are pretty inventive.
Improve your visual literacy
Just found a very nice series of blog posts on beginning graphic design from 2008:
Very clear presentation, very worth reading through to improve one's visual literacy.
Infinity, 5 or 3?
After dinner discussion yesterday: which of the terms in this series stands out?
1, infinity, 5, 6, 3, 3, 3, 3, ...
An extra challenge (below the fold) is of course to tell what generates it.
The series corresponds to the number of regular convex polytopes in different dimensions. In one dimension there is just one (a line segment), in two there are an infinite number of regular polygons, in three there are five platonic solids, in four there are six, and then there are just three (the n-simplex, the n-cube and the n-orthoplex).
In our discussion several views came forth: Infinity is the unusual term, since it is not even a number. 5 and 6 are unusual, since they are non-trivial numbers - 1 and infinity are just a "transient" at the start (it usually takes more bits of information to specify a number "somewhere in the middle" than 1 or infinity). 3 is the unusual number, because it is repeated indefinitely - everything else is just a transient (my position).
If we allow nonconvex regular polytopes, we get the sequence
1, infinity, 9, 16, 3, 3, 3, 3, ...
There are no nonconvex regular polytopes in five dimensions or more. The nonconvex polytope sequence seems to support me - three again!
Of course, the whole question is ill-defined and somewhat pointless, but all the best Oxford postprandial debates are like that. I love starting arguments about
what the river passing the town "really" is named (and of course what kind of object a river name signifies - are rivers physical things, locations, processes, social constructs or something else?)
Overall, it seems to me that what is going on here is that low-dimensional spaces have pretty trivial symmetries only allowing zero, one or an infinity of some class of objects. 3 and 4 dimensions are unusual in that the extra degrees of freedom makes a non-trivial number of objects possible yet do not allow the infinite sets of 2 dimensions - sometimes more is less! In the higher dimensions things tend to smooth out, but I find it odd that the symmetries of space do not end up allowing an infinite number, zero or a single object in this case.
August 23, 2010
This and that
My bank webpage has *opening hours* for some subsections, a quite remarkable concept that completely negates most of the point.
I just finished making the first version of my own website for Eclipse Phase texts.
Tarte Tatin is hard to beat as a dessert.
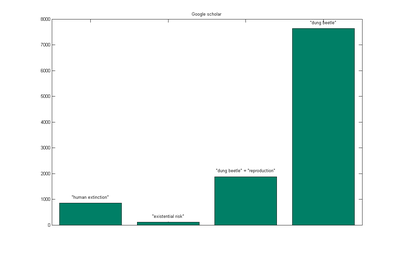
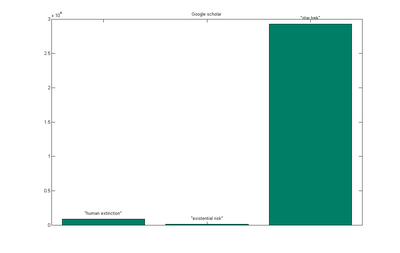
Rebecca Roache rechecked my survey for the truth of Nick Bostrom's claim "there are more papers on the reproduction on dung beetles than about the risk of human extinction". Looking at ISI, Scopus and Google Scholar this seems to hold true- Due to the nature of search, this kind of survey will tend to overestimate human extinction papers ("human extinction learning" etc will cause overcounting) and underestimate the dung beetles by not using their correct taxonomic names).
Another glaring comparison: scholarly papers on Star Trek and human extinction.
Not that Star Trek or Scarabaeinae are uninteresting or unimportant research topics. But it is a bit embarrassing we are spending so little effort on ensuring our own survival.
August 19, 2010
Ego vs environment
Numeracy vs. feel-good (Practical Ethics) - I blog about the PNAS paper showing that people are bad at estimating energy savings. Basically a continuation of my jihad against lack of innumeracy and lack of proportion.
I wonder how much of people preference for curtailment rather than efficiency increases is due to anti-modernity sentiments and propaganda? It could be, as I argue in the other post, that it is just because curtailment has immediacy that people go for it as the better choice, but I suspect at least some thinks it is more virtuous to go without. Which doesn't help the environment, but does stroke their own self esteem.
August 14, 2010
Skiffy Cover
Damien Broderick's latest volume Skiffy and Mimesis is appearing. With a cover by yours truly.
Those pentapods do get around.
In other graphics news I put some renderings on Flickr of a Bernal sphere habitat, Mathias Chikawe Station, from my Eclipse Phase campaign. Here is an exterior and interior shot. By no means the most exciting outside, but the interior is pretty fun. I am just worried that most of the mass you can get in the ring system is going to be ice: while there are a bit of tholins to build from, you will need to important heavier materials from the outer moons.
August 13, 2010
Sing, O goddess, about the ultimate mashup
"Helen of Troy awakes just before dawn to the sound of air raid sirens."
That is one of the best opening lines of a novel I have ever read. Dan Simmons' Illium and Olympos (the line is from the later) are very well written novels, which is fitting since they on a deep level are about stories and their power. They are also dense, crammed with references and sometimes infuriatingly more interested in literary details than making sense.
Just as our civilization would leave amazing piles of comics, computer games, bizarre art pieces and radiated television shows behind if it disappeared, so have the posthumans of the novels littered the solar system with strange things: a mysteriously rapidly terraformed Mars, double rings of paradisical orbital cities around Earth, a chasm across the Atlantic, continent-spanning steampunk transport systems, Shakespearean protagonists with near-divine powers, an ongoing Trojan War and, indeed, quarrelsome Greek gods living on Mount Olympus and shooting down passing spacecraft. Resurrected scholars monitor the progress of the Trojan War, bourgeois eloi spend their time on Earth flitting around parties and in the outer system the moravec cyborgs debate literature. It is a total mess, and would in lesser hands likely make a very silly setting. Simmons manages to pull it off, but just barely: this is an extremely epic story (the *Illiad* is just one of the subplots!), but so epic and literary that it is nearly absurd.
Being an avid hard sf reader I found the moravecs the most appealing characters. Literature- and engineering-minded by design, they have a thriving civilization in the outer system but little contact with whatever is going in the inner system. As they get concerned about the weirdness and start investigate they act as the classic outside view, helping the reader (at least the reader based in hard sf) figure out what is going on. They are rational without being dogmatic: if a Greek god flies by in a chariot they will accept it and try to make some measurements. In many ways they are far more like us the readers than the "normal" people living on Earth, who have a culture and lifestyle supported by unseen technologies to the degree that many human universals seem to have broken down.
The novels can be seen as ambitious mashups: Homer meets Shakespeare meets Nabokov meets Proust meets Shelly. Many characters speak and act based on things in other works of literature: just as there exist parallel worlds in the in-story physics, the literary parallel worlds interact with the Illium/Olympus world. Which makes it somewhat confusing if you haven't read the originals (and who, honestly, has read Shelly's Prometheus Unbound?) On the other hand, this is after all what many people reading "real literature" enjoys - just as I enjoy noticing hard sf authors having done their physics homework and maybe run a few simulations to test their models. This kind of densely intertextual and referenced story might be just what posthumans would be telling each other: every strange turn of phrase or quote can be instantly googled and maybe also directly contextualized.
In the end, I think the key insight I got from these novels was that a healthy future posthuman futures are likely to be baroque rather than sleekly modernist. There will be more culture around, easier ways of accessing it, easier ways of expressing culture materially. Even if a small fraction of the civilization cares, that will still produce enormous amounts of very strange artefacts. Homer would likely find these novels prime examples.