Andart

My 0.15 MilliDarwins of Fame

The Science Hall of Fame uses Google's ngram-viewer to calculate fame of scientists, based on how often they are mentioned in books. The unit of measurement is the milliDarwin, being mentioned a thousand times less often than Charles Darwin.

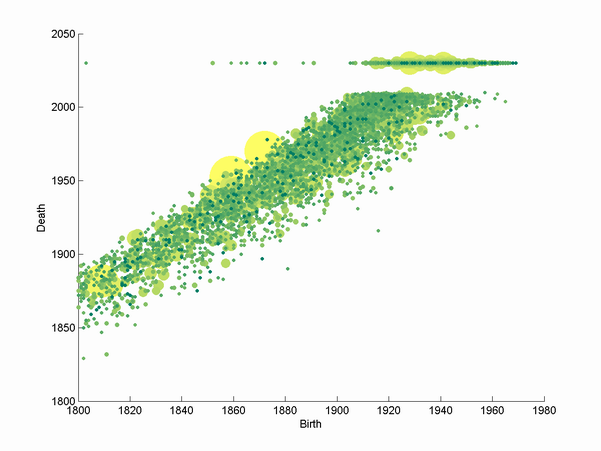
Plotting fame versus birth and death (and still living scientists as a separate line above) shows that fame doesn't seem to be that strongly clustered in time. There is actually no tendency for long-lived researchers to have a high ranking, which surprised me.

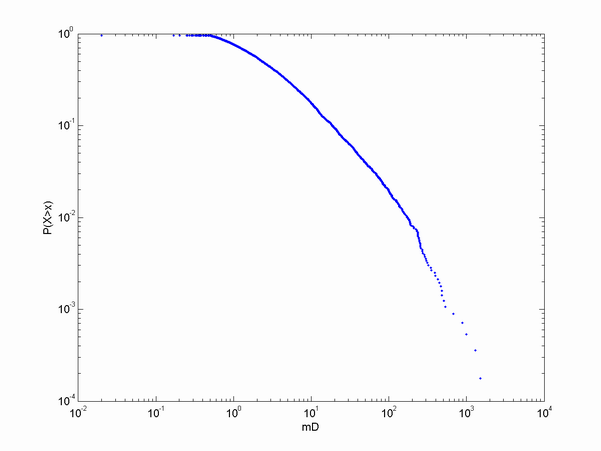
Most surprisingly, the distribution of fame is not a power law distribution. It is very skew, but looks to me more like a stretched exponential distribution. Perhaps people are more explicit when referring to obscure or normal scientists, while references to Darwin or Einstein are left implicit.

As for myself, I estimate my scientific fame to be 0.15 mD. This is a bit of guesswork, since google Ngram viewer doesn't show books after 2002, and I have good reasons to suspect more has been written mentioning me recently than before 2002. Also, I am conflated with several other Anders Sandbergs. Looking at the Google books hits, I estimate that I am the target of around 36%. But I am not surprised that I am small fry. So far.

How dangerous is it to be in a crowd?

A friend of mine worried about public transport, given the existence of "feral" humans who might attack neighbours. Turns out that elevators are worse.

The risks are pretty low. Looking at UK statistics and dividing the crimes by population there is a risk of 9.58*10^-5 per day to suffer "other theft", 7.36*10^-6 for robbery, 4.64*10^-6 for sex offence, 3.75*10^-5 for "violence against person with injury" and 4.19*10^-5 for "violence against person without injury". Some of these crimes would of course have had more victims, but as a conservative guess the total risk of being a victim of a personal crime is likely less than one in 10,000 per day.

Assume a fraction p of people are bad guys who will do something nasty. Fortunately, p is generally a small number (both because bad guys are rare, and because they act badly only occasionally). In a crowd of size N there will be on average Np bad guys (assuming there are no correlations). The probability of being in an entirely nice crowd is (1-p)^N, which approaches 0 as N grows.

What is the risk of being subjected to the activities of the bad guys in the crowd?

If each bad guy victimizes just one person, then the probability of being the victim of him is 1/(N-1) (since bad guys rarely victimize themselves). Here I assume they select victims entirely at random in the crowd, which is untrue but simplifies things. There will on average be Np crimes, so you would on average suffer Np/(N-1) crimes (yes, this assumes you have a probability p of being a bad guy too).

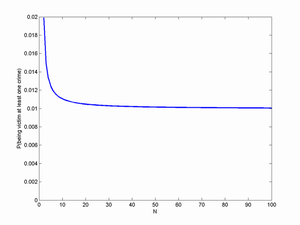
As N becomes large, this approaches p - being in a large group might mean you are almost certainly in the presence of criminals, but you are unlikely to be their victim. However, for N small the risk goes up! This is because now the pool of potential victims is smaller: in the case of you being the only other person the criminal will choose you. Elevators are dangerous.

A more careful analysis: the risk of being victim of at least one crime if there are k bad guys is 1-(1-1/(N-1))^k = 1-((N-2)/(N-1))^k. The probability of k bad guys out of N people is (N over k) p^k (1-p)^(N-k), so the total expected risk is sum_k=1^N (N over k) p^k (1-p)^(N-k) (1-((N-2)/(N-1))^k). Since p is small one can approximate this as a Poisson distribution. Here is a plot for p=0.001.

However, these are one-to-one crimes. What happens if we worry about bad guys doing things that affect groups of people?

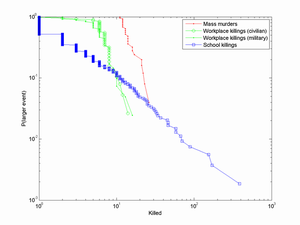
A plausible distribution of the number of victims for acts of random violence is a power law distribution. This follows from Richardson's celebrated study of "deadly quarrels", as well as modern studies of terrorism. So the probability of X victims would scale as P(X)=CX^-a (1<=X<=N), where a is a scaling exponent and C a normalizing constant. This is likely true for other kinds of multiple crimes too: here is an empirical distribution plot of mass murders, workplace killings and school shootings (data from Wikipedia) - it looks like they have power law tails.

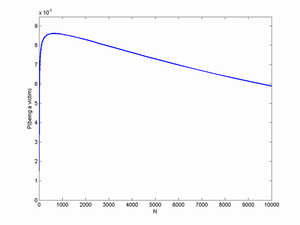
In a crowd of N subjected to a size X attack, the risk of being a victim is X/N. If there is one terrorist attack it presumably precludes another (or they can be viewed as joined together, it doesn't seem to matter). The risk of an attack grows as 1-(1-p)^N. Putting all this together we get the following kind of plot (here p=0.0001):

There exists a maximally dangerous crowd size, where the chance of an attack is relatively large but there is a decent chance that you will be among the victims.

Of course, this p is absurdly large. Let's guess that the real p is 10^-10 (there are probably about a thousand terrorists in the world out of 7 billions people, each doing an attack at most once one day out of every 3 years or so). This produces a most dangerous group size of about 6 million people, with a risk to you almost 1 chance in 10¹⁰.

The actual empirical risk worldwide per day of being a victim of terrorism is 4.76*10^-9 (there are ~1.47 attacks per day anywhere in the world, on average killing 22.66 - in fact, in 37% of the attacks nobody gets killed). So there is no real reason to worry about terrorism compared to the risks of getting to the group (traffic; in the UK the risk of being killed is about 10^-7 per day) or being there (riots, infections).

But stay away from elevators. Even if you are a bad guy.

Now back on track

Sorry for the recent blog outage. The cause was not snow or flooding, but simply the annual payment confusion - living in a different country from your ISP and moving does complicate things.

In other news, I blogged on the freshly revamped Practical Ethics about whether DIY enhancement is morphological freedom or self-harm. My basic view is that while it could be a form of self-harm and that there are forms of enhancement that are a bad idea to do, there are forms of even fairly squicky DIY self-surgery that are legitimate morphological freedom.

Improbable Win

Now I have finally reached the pinnacle of academic fame: TV Tropes links to two of my papers! (in the Real Life section of the page "Unrealistic Black Holes").

I guess the weird probability going on in the papers is really a disproof of many real-life attempts at If My Calculations Are Correct. Or maybe You Fail Statistics Forever. Of course, TV Tropes actually has an entry on The Anthropic Principle, which is pretty cool - this was once a rather esoteric philosophical subject, but now it shows up in plenty of popular fiction.