November 14, 2006
Minimal Double Walls
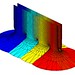
Yesterday when playing around with the Enneper-Weierstrass formula for minimal surfaces. I plugged in g(z)=tanh(z) and f(z)=1, producing this nice minimal surface.
It is parametrized by [a,b,c]=Re[tanh(z),i*(2z-tanh(z)), 2ln(cosh(z))].
The basic structure is neat and simple. An almost plane surface bends like a book spine, erupting in an infinite number of catenoid flares. These rudely intersect as catenoids are wont to do, preventing embedding. It is topologically equivalent to an infinitely punctured plane due to all the singularities at ±(2n+1)π/2. Each singularity causes a flare from the bending region.
I have not seen this minimal surface before. Trying g(z)=cosh(z) and g(z)=sinh(z) produces what I think is the Henneberg nonorientable surface. But it seems unlikely that something as obvious as tanh(z) could have been overlooked, so I wonder what this surface is called.
One explanation might be that it doesn't have many useful properties: while the planes look inviting for building something they are very gently undulating rather than being perfect planes and hence cannot be mirrored to produce another line of flares. Still, my surface looks like a limiting case of the k-Noid as k goes to infinity.
Drawing it nicely posed a few problems. Just using a rectangular mesh produced jaggedness close to the singularities. In the end I had the idea of using both a rectangular point grid to get the overall plane part nicely triangulated, and adding radial point grids near the singularities. Then I used a Delaunay triangulation to form the base mesh.
Posted by Anders3 at November 14, 2006 02:07 AM