July 08, 2006
The Best (Spill-free) Coffe Cup is Elliptic
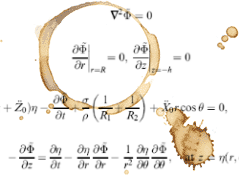 How to make a coffee cup that doesn't spill easily when filled to the brim? Walking often sets up resonant sloshing (seiching) that makes it overflow. Of course, adding lids, inward-sloping edges or perforated slosh-baffles solves the problem easily, but at the price of inelegance or making the cup harder to wash. The most elegant approach would be to get rid of the sloshing eigenmode that causes spilling.
How to make a coffee cup that doesn't spill easily when filled to the brim? Walking often sets up resonant sloshing (seiching) that makes it overflow. Of course, adding lids, inward-sloping edges or perforated slosh-baffles solves the problem easily, but at the price of inelegance or making the cup harder to wash. The most elegant approach would be to get rid of the sloshing eigenmode that causes spilling.
Linear Sloshing
The movement of a non-rotating, incompressible sloshing liquid in a cylindric vessel is described by a velocity potential obeying Laplace's equation. The time dependency creeps in through the free surface boundary condition, something I can't get my head around. Following this example we get the normal modes
Φn,m=Jm(αn(m)r/R)(Amcos(mθ)+Bmsin(mθ))cosh(αn(m)r/R)cos(ωn,mt)
where h is the liquid height and R the radius of the cup. αn(m) are the n'th positive root of the m'th order Bessel function Jm(x).
ωn,m = gαn(m)tanh(αn(m)h/R)/R
producing the frequencies
sqrt(gαn(m)tanh(αn(m)h/R)/R)/2π Hz
for the modes. (see the bottom of this page for animations).
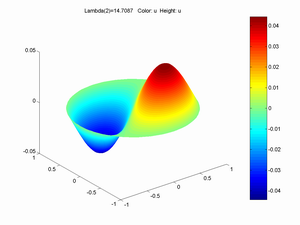
It is the lowest frequency antisymmetrical modes that tend to get excited by walking, and the n=1,m=1 mode is the classic sloshing back and forth mode. In the example above it has frequency 3.38 Hz.
An obvious solution based on this is to make the cup higher and narrower. Halving the radius about doubles the frequency. This is why espresso is less likely to be spilled than ordinary coffee. Higher cups also increases the frequency but just with the square root of the height.
Another trick is to stir it with a spoon to give the liquid angular momentum; this forces the liquid to behave according to the m=0 radial modes.
High Frequency Low-Frequency Eigenmodes
Back to the eigenmode approach. We want to make sure that the n=m=1 mode frequency isn't a low multiple of our walking speed.
Walking corresponds to driving the oscillations in the cup with a driving force of some shape, fortunately mostly vertical. The natural frequency of a leg is sqrt[3g/2L] Hz, about 0.64 Hz, supported by empirical studies. Walking is faster (2 legs, after all), around 0.9-1.3 Hz - the
exact frequency depends on walking speed and length. This variability of course shows another easy way of avoiding sloshing, just walk slower or faster, it just costs a little bit more energy.
I played around with the partial differential equation solver pdetool in Matlab to see what happens to the eigenvalue of this mode if we change the cup shape slightly. Of course, the above solution is not really valid in these cases, but clearly something very similar would hold. An increase ω' = kω of an eigenvalue would increase the corresponding frequency by sqrt(k).
Breaking the circular symmetry makes the symmetric eigenmode split into two orthogonal modes, one corresponding to sideways sloshing and one to forward sloshing. If the sideways mode has lower frequency it is will likely get more of the walking energy than the forward mode, and hence reduce overall spilling.
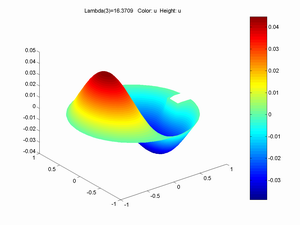
First I tried adding indentations in the circular border. A 0.25R square at one side increased the eigenvalue by 1.11, just a 5% increase in frequency. Adding a similar square on the other side gave a 12% increase. Making the squares diamonds had even smaller effects. Making the square a long thin divider brought up the frequency by 16% and forced the velocity bump to split.
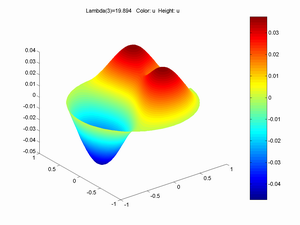
Making the cup elliptic had better effect. Making it a 3/4 ellipse with the broad side in the shaking direction gave a 25% frequency increase. An even better effect was to make the cup the union of two circles withb radius 0.75 and centre separation 1. Now the seiching mode we want to avoid is 26% higher frequency, but there are two lower frequency sideways eigenmodes that can take up energy too.
To sum up, making eigenmodes too high frequency to couple to walking is probably hard to achieve by small changes in cup shape unless you happen top have a very particular walking frequency. Making the cup shorter in the travel direction can however drive up the sloshing frequency significantly and likely reduce spilling.
Some further linear sloshing links:
James
G. Seebold: Flare pulsation due to seal drum sloshing