Andart

Ring the bells of freedom

My colleague Brian Earp blogs on Slate about What if Technology Made "Gay Conversion Therapy" Work?, based on an upcoming paper by us.

I have always been concerned when people defend gay rights based on sexual essentialism: that our preferences are unyielding and unchangeable. The claim is not really well supported empirically. One does not need to buy into wishy-washy relativism or tabula-rasa ideas to conclude that at least some aspects of sexual preferences are plastic and can be changed by ourselves or our conditions. So while "born this way" makes a good rhetorical club, it is not necessarily a good argument against discrimination.

A much better argument is that what two (or more) consenting adults do in private is their own business. This is independent of what the actual neuropsychosociology of sexual preference is - and covers far more ethical cases.

Distance between planets

A question that came up recently: what is the average distance between two planets orbiting a star at radius R1 and R2 in circular orbits?

If we rescale things in units of R1, so planet 1 orbits at distance 1 and planet 2 at distance r=(R2/R1), the answer for the average is =(1/2pi) times the integral from 0 to 2 pi of sqrt((cos(x)-r)^2+sin(x)) dx... which unfortunately is only expressible in terms of the elliptic function of the second kind. Possible to calculate, but messy and hard to understand:
=(1/Pi) (Sqrt[(-1 + r)^2] EllipticE[-((4 r)/(-1 + r)^2)] + Sqrt[(1 + r)^2] EllipticE[(4 r)/(1 + r)^2])
Even implementing this calculation in software that has the function in the library needs some care, it is easy to slip up with some term or modulus somewhere.

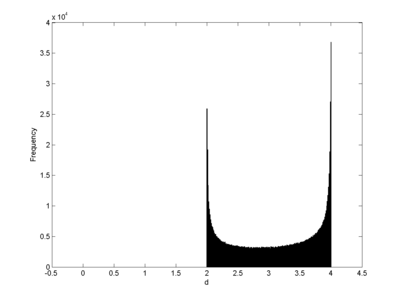
However, a quick Monte Carlo simulation gives some nice results. First, the distribution has more probability mass close to the extremes than near the middle. Here is how it looks when r=3:

Most of the time the planet is either on the far side or the close side of the sun by the reckoning of the other planet. So the average distance is somewhat misleading in the first place: the mode (the most probable point) is that it is on the other side, but the distribution is properly bimodal.

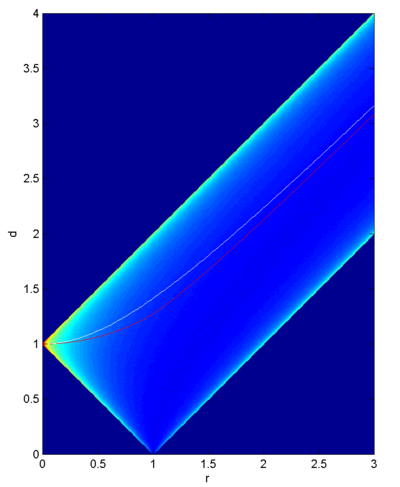
Plotting the distribution as a function of r gives the following nice picture:

The colors denote probability density. For r=0 it is all located at distance 1. Then the possible range increases linearly, until r=1 and it briefly becomes possible for the planets to coincide (maybe not the most physical situation). As r becomes larger the distribution is all housed in the strip [r-1,r+1].

The red and white line indicate the median and mean, respectively. As we can see, they are not terribly representative of where the other planet actually is.

It turns out that the median curve can be approximated surprisingly well by 1+r^2/(1+r). The absolute error starts out as 0 for r=0, reaches a maximum of 0.1 for r=1 and then declines.

For large r the probability distribution becomes more symmetric converges to the arcsine distribution. The median and mean converge to r.

So a good guesstimate for the median distance is R1*(1+(R2/R1)^2/(1+(R2/R1))) = R1 + R2^2/(R1 + R2). It is not exact, but given that the actual distance is likely to be R1 away from it anyway, it is good enough for many purposes.

Placebo polygraphs

Polygraphs: placebo or trial by ordeal? - a Practical Ethics post where I argue that it is ethical to train people to deceive polygraphs.

The short version: polygraphs are lousy deception detectors, and relying on them causes both false positives, allows all sorts of biases to influence decisions, promotes false confessions, and worst of all, relies on deliberate deceit about their power. They are essentially a placebo technology, so teaching people how to beat them - or just the fact that this is possible - improves the overall epistemic standards.

Finding happiness

Sometimes you learn a new fact that immediately makes your life go better. It happened to me this week, and now I want to tell you.

I found Shift + Ctrl + T.

This will undo closing a tab in a web browser. The sheer amount of low-grade frustration and lost time accidental closing generates is enormous, yet distributed so that few take action: it is death by papercuts. But this keyboard shortcut solves it quickly and neatly.

It is a sad fact that many people today do not learn keyboard shortcuts. They deserve the name, especially since they can be activated without moving your hands from the keyboard. You do not need to know all of them, just the ones that help you - but to do that you should explore how to trigger your favourite commands. The only thing more immediate might be gesture control using the mouse in mouse-oriented applications.