March 09, 2014
Are superstars good? Fame vs. merit
Yesterday I looked at fame distributions and their inequality, concluding that they are very unequal. But maybe merit is just as unequally distributed too? After all, Norman Borlaug saved hundreds of million of lives, while most of us can hardly claim to have saved even a single one. So I wanted to see if a reputation system could track actual merit, or the rich-get-richer aspects of being well-known would swamp it.
My model is as follows: people arrive to a group, selecting 5 people to adore. Each person has a merit that is distributed as a x-2 power law, and a fame corresponding to the number of people adoring them. The new people select targets with a probability proportional to a weighed combination of their normalized apparent merit plus their normalized fame: how much they weigh merit over fame is one of the parameters of the model. The apparent merit is the real merit combined with random noise; the amount of noise is the other parameter.
Since each new person can only choose from earlier persons, there will be some bias towards the first-comers even if they have low merit. In the case of not caring about merit at all it is just a preferential attachment process where we get celebrities famous for being famous.
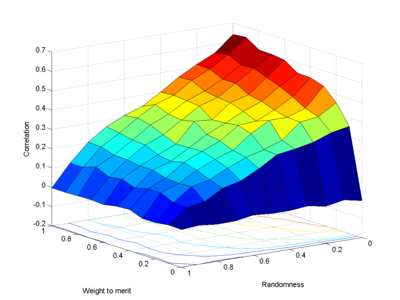
Running it for a 1000 person population, repeating 10 times and plotting the average correlation between log(merit) and log(fame) for everyone (logarithms since these things range over several orders of magnitude) we get the following effect:
Most obviously, as the randomness decreases from left to right, the ability of the people to discern who has merit or not improves. Total noise (randomness=1) produces zero correlation between them. Similarly improving weighting of merit improves discernment - zero weight also produces populations with celebrities of random merit. As they weight merit more, merit and reputation become more correlated.
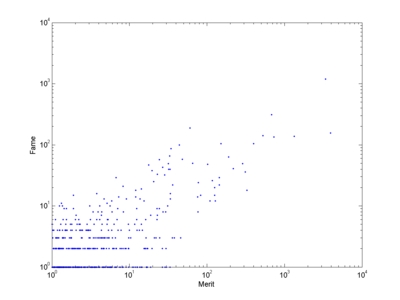
But even for zero noise and everybody basing their choice solely on merit, the correlation only becomes 0.7. Superstars may not be mediocre, but there is no guarantee they are the best, as can be seen below. Some diamonds are still hidden in the rough, and the best person is not the most well-known.
One could argue that this is because people in my model select people to adore stupidly. They just select people with a probability proportional to actual merit, not just the top 5 people. But in real life we rarely spend time finding the best target of our admiration - we have limited time, attention and information and hence will make choices from smaller sets of candidates than we should (after all, how many have heard about the scientists greater than Einstein?) So I think my simple model gets things roughly right: limited agents will not achieve a perfect match between reputation and merit, even when they are unbiased by celebrity and noise. And the real world case is likely far worse.
So reputation economies will not be able to achieve a strong match between reputation and actual merit. They can achieve correlation, but one can argue this is true for current economies too (I tend to sell more if I make stuff that people like rather than stuff they hate). The argument that capitalism distorts this because you can make more by investing rather than being good obviously applies to reputations too: if you are well-known, you can more easily get people to notice your latest good deed. The nature of attention simply tends to bias us towards a few superstars.
Posted by Anders3 at March 9, 2014 07:47 PM