July 29, 2013
Summer Silence
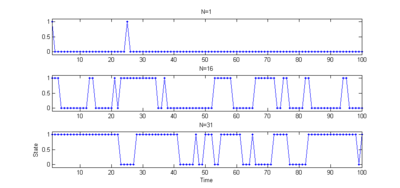
Summer means many mailing lists and forums die. Here is a small model of what is going on:
When list members see activity they become more likely to post, maintaining activity. When there is no activity they often forget about the list, and have a much lower probability of posting anything (typically "Test: is this list dead?").
We can model this as N people, each with independent probability p of posting if they saw activity over the past day, and probability q << p of posting in the case of no activity.
This model also describes the "critical mass" problem of creating new forums - whether it is bootstrapping a big social network or just getting the researchers in a project to talk to each other online on the official forum.
A simple approach is to argue that N people will on average produce Np messages, and as long as Np>1 we will stay in a high activity state: each post is likely to trigger at least one post next day. As summer arrives N and p decreases due to holidays and laziness, and we cross the threshold in many forums to the low activity state, where the average number of posts is Nq. The time until such a post happens is around 1/Nq.
A slightly more ambitious model is to view it as a Markov chain with two states, "active", "inactive". The probability of no posts today if we are in the high activity state is (1-p)^N, and that moves us to the low activity state. We stay there as long as things are quiet, which has probability (1-q)^N. As long as q>0 this state is not absorbing, and eventually we go back to the active state. Writing out the other transitions results in a 2x2 state transition matrix, and one can use the standard textbook methods of solving it.
In particular, as shown here for this kind of simple 2x2 case we can do it by hand and get the probabilities as:
P(active) = (1-(1-q)^N)/(1-(1-q)^N+(1-p)^N)
P(inactive) = (1-p)^N/(1-(1-q)^N+(1-p)^N)
While the formulas are pretty messy, a plot makes things clear:
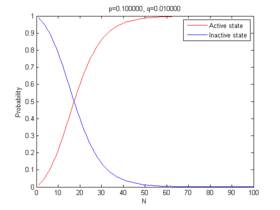
We get the transition point at 1-(1-q)^N=(1-p)^N (around 17 in this case). The transition is by no means sharp. Even smaller and quieter lists do have activity, it is just that on average it tends to end relatively quickly:
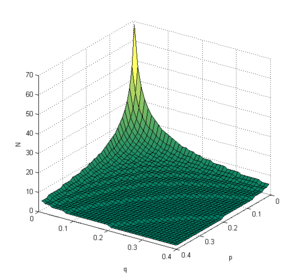
Plotting the required number of participants as a function of p and q gives us the following plot:
Note that you only need a very small group if people post a lot. Having people who add new stuff even with no prompting (high q) is just as good as having talkative people in the active state, in terms of maintaining critical mass.
However, the residence time in the active state behaves as a geometric distribution with expectation 1/(1-p)^N. The residence time in the quiet state has expectation 1/(1-(1-q)^N). The ratio of quiet time to talk time, (1-p)^N/(1-(1-q)^N) is not symmetric in p and q. It is more sensitive to q for small N: if you can boost the spontaneous posters, you make it more likely they will jumpstart the list out of a quiet state and then the normal posters will keep it up. For large N this is not often required, and increasing p is more effective in keeping the flow going.
So, the trick to end the summer silence and jumpstart small forums is to post something. And keep up doing that even if nobody responds the first time. On large forums that have gone quiet the problem is more likely that few want to say anything. That requires other methods.
Posted by Anders3 at July 29, 2013 01:42 PM