Andart

Evolution and the aliens

My friend Milan M. Cirkovic gave a talk here last week on Evolutionary Contingency and the Search for Life Elsewhere. It is now on YouTube:

Some people wonder why we at FHI care about alien life. But as Milan shows, there are some pretty profound links to existential risk and deep philosophical questions about the nature of intelligence, what we can observe, and what we might change into.

I will be a bit nicer to science journalists in the future

Spin city: why improving collective epistemology matters | Practical Ethics - I riff on the recent paper showing that there is plenty of spin already in the paper abstracts in science, adding to the existing distorting effects of science reporting.

Figuring out how to make our collective information processing better matters a lot, especially when it comes to science. If the reporting and understanding of the results is bad, that means that our decisions will be distorted - including further decisions about what is important to fund or report on. I suspect that the impact on total knowledge production and dissemination even from a slightly better collective epistemology would be significant. Research funding bodies might be better off funding development of better trust and reputation systems than many currently fashionable topics, if only to create an environment where it becomes easier to tell what is actually worthwhile.

Me in Tallinn

I give a little talk about cognitive enhancement: Shifting Your Brain: Anders Sandberg at TEDxTallinn - YouTube

Flaws in the perfection

Gwern Branwen has a great essay, The Existential Risk of Mathematical Error where the problem of mathematical errors is dealt with.

As we argued in our probing the improbable paper, complex scientific arguments are untrustworthy because there is a finite probability of mistakes at every step. There are estimates that at least 1% of all scientific papers ought to be retracted. When explaining this to a mathematician friend, he responded that he thought a far smaller number of papers in math were this flawed. It seems that he should not have been so optimistic.

But Gwern points out that type 1 errors, where the claim is true but the proof doesn't work, seem to be more common than type 2 errors, where the claim is false and the proof is erroneous. This is good news. Although I am not entirely convinced that we have sufficiently long and unbiased data to make a firm judgement. Another interesting aspect is that type 2 errors have often precipitated mathematical revolutions by showing that intuitive insights are wrong and the world is stranger than we expect.

Unfortunately I suspect that the connoisseurship of mathematicians for truth might be local to their domain. I have discussed with friends about how "brittle" different mathematical domains are, and our consensus is that there are definitely differences between logic, geometry and calculus. Philosophers also seem to have a good nose for what works or doesn't in their domain, but it doesn't seem to carry over to other domains. Now moving outside to applied domains things get even trickier. There doesn't seem to be the same "nose for truth" in risk assessment, perhaps because it is an interdisciplinary, messy domain. The cognitive abilities that help detect correct decisions are likely local to particular domains, trained through experience and maybe talent (i.e. some conformity between neural pathways and deep properties of the domain). The only thing that remains is general-purpose intelligence, and that has its own limitations.

Maybe a sufficiently smart mind would indeed be able to learn the patterns in such messy domains and develop a nose for them (this might be less a case of superintelligence and more a need for very large amounts of data and learning, but it could also be that very clever representations are needed to handle and learn this much data).

In the meantime, we should learn how to sniff out type 2 errors. They are the most valuable discoveries we can make, because they make us change direction.

Nukes, Silver Medals, PERT, and Galton

It took the Soviet union 48 months after Trinity to detonate their own atomic bomb. It took them about 9 months after the US detonated their hydrogen bomb to detonate one of their own. The US needed about three months to launch their own first satellite after Sputnik.

If there are several groups racing towards the same goal, what is the distance between the winner and the second place?

Simulations

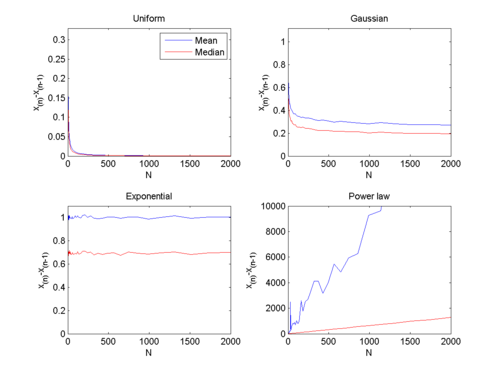
Empirically we can see the following, by running 10,000 trials where we look at the difference between the largest and second largest random number drawn from different distributions (this would correspond to the amount of progress achieved until the winner reaches the unknown finishing line):

If the random numbers are uniform the the distance between the winner and the second in place is a rapidly declining function of the number of participants.A large competition will be a close one.

If the success is normally distributed, the distance is a slowly decaying function of the number of participants. Large competitions can still leave a winner far ahead.

If the success is exponentially distributed, then the average distance is constant.

If the success is power-law distributed as P(x) = Cx^-2, then the distance grows linearly with the number of participants. The more participants, the more likely one is going to be to have a vast advantage.

One could of course view the random numbers as project completion times instead, and look for the minimum. This doesn't change the uniform and normal distribution cases, while the exponential and power-law cases now look much like the uniform: it doesn't take a large number of competitors to produce a small distance between the winner and second best.

The real world

In real life, project completion times are likely a mix of a Gaussian with some heavier tail for long delays, but this depends on domain. At least some project management people seem to assume something like this (scroll down). One paper found inverse Gaussian distributions at an automobile plant. PERT people appear to have a model that uses a three-point estimation to make a distribution that is kind of parabolic (I would believe this as a plot of the logarithm of probability).

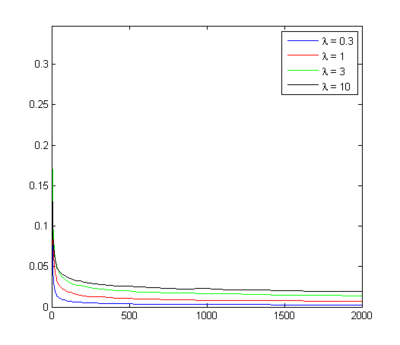
Inverse Gaussians make sense, since this is the distribution of the time it takes for Brownian motion to get above a certain level if starting from 0: consider the progress of the project as Brownian, and completion times become inverse Gaussians. Here is what happens if we look at the difference between the fastest and second fastest project when their times have inverse Gaussian distributions with μ=1 and different λ (corresponding to different drift rate variabilities; high λ is close to a Gaussian):

This is somewhere between the uniform case (where you are confident the project can be completed within a certain time) and a Gaussian case (there exists some unknown time when all tasks have been completed, but there are many interacting effects affecting progress). So I think this speaks in favour of numerous competitors leading to closer races, but that the winner is often noticeably far ahead, especially if the number of competitors are smaller than 10.

In real situations things become even more complex in technology races because projects may speed up or slack off as they get ahead or behind (there is a literature on this, trying to figure out the conditions when it happens). Projects may cooperate or poach ideas from each other. Ideas might float in the general milieu and produce near-simultaneous discoveries.

Proving stuff

Leaving the original question and moving towards the math: how to determine what happens as n increases?

One way of calculate it is this: The joint distribution for the n-1:th and n:th order statistics is

f_X(n-1)X(n)(x,y) = n(n-1) [F(x)]^n-2 f(x)f(y)

where f is the probability density function of the random variables and F is the cumulative on. So the expected difference is

E(X_(n)-X_(n-1)) = n(n-1) ∫ ∫_x≤y (y-x) [F(x)]^n-2 f(x)f(y) dx dy

Lovely little double integral that seems unlikely to budge for most distribution functions I know (sure, some transformations might work). Back to the drawing board.

Here is another rough way of estimating the behaviour:

If F is the cumulative distribution function of the random variable X, then F(X) will be uniformly distributed. The winner among n uniformly distributed variables will on average be around (n-1)/n. The second best would be around (n-2)/n. Transforming back, we get the distance between the winner and second best as:

E[X_(n)-X_(n-1)] = F^-1((n-1)/n) - F^-1((n-2)/n)

Let's try it for the exponential distribution. F(x) = 1-exp(-λ*x). F^-1(y) = -(1/λ) log(1-y).

E(X_(n) - X_(n-1)) = (1/λ) [ -log(1-(n-1)/n) + log(1-(n-2)/n) ]
= (1/λ) log [ (1-(n-2)/n) / (1-(n-1)/n) ] = (1/λ) log(2)

Constant as n grows.

What about a power law? F(x) = 1-(x₀ / x)^a (a<0) (note that this a is one off from my formula in the simulation!), so F^-1(y) = x₀ (1-y)^-1/a.

E(X_(n) - X_(n-1)) = x₀ [ (1-(n-1)/n))^-1/a - (1-(n-2)/n)-1/a ] = x₀ [ n^1/a - (n/2)^1/a ]

If we let a=1 then the difference will grow linearly with n.

Uniform? F(x)=x, so F^-1(y) =x and E(X_(n) - X_(n-1)) = (n-1) - (n-2) / n = 1/n.

That leaves the troublesome normal case. F(x) = 1/2 (1+erf(x/sqrt(2))). So F^-1(y) = sqrt(2) erf^-1 (2y-1), and we want to evaluate

E(X_(n) - X_(n-1)) = sqrt(2) [erf^-1(2(n-1)/n-1) - erf^-1(2(n-2)/n -1) ] = sqrt(2) [erf^-1(1-2/n) - erf^-1(1-4/n) ]

Oh joy.

Using that the derivative is (sqrt(π)/2)e^erf-1(x)2 we can calculate an approximation by using the first Taylor term as E(X_(n)-X_(n-1)) = (sqrt(2π)/n)e^{erf-1(1-4/n)2}. Somewhat surprisingly this actually seems to behave as the Gaussian in my simulation, but I still can't say anything about its asymptotic behaviour.

I'm not even going to try with the inverse Gaussian.

Into the library

It is said that a month in the lab can save you an hour in the library. The same is roughly true for googling things. But usually you need to dig into a problem a bit to find the right keywords to discover who already solved it long time ago.

In this case, I had rediscovered Galton's difference problem. Galton posed the question of how much of a total prize to award to the winner and to the second best in a competition, so that the second best would get a prize in proportion to their ability. (Galton, F. (1902), ”The Most Suitable Proportion Between The Values Of First And Second Prizes”, Biometrika, 1(4), 385-390) It was solved straight away by Pearson in (Pearson, K. (1902), ”Note On Francis Galton’s Problem”, Biometrika, 1(4), 390-399.), who pioneered using order statistics to do it.

Since then people have been using this in various ways, approximating the statistics, allocating prizes and thinking of auctions, estimating confidence bounds and many other things.

In any case, the formula is

E(X_(r+1)-X_(r)) = [Γ(n+1)/Γ(n-r+1)Γ(r+1)] ∫ F(x)^n-r[1-F(x)]^r dx

Plugging in r=n-1 gives us the desired distance. Although the integral is still rather tough.

Conclusion: figuring out that what is needed is order statistics is not terribly hard. Figuring out where I can find asymptotic expressions for erf^-1 near 1 is trickier. We need to have a maths concept search engine!

(Incidentally, those early issues of Biometrika were cool. Smallpox vaccination, life expectancies of mummies, new statistical concepts, skull measurements, all mixed together.)

The scale of progress: why we are overconfident about our ability to judge feasibility

Comprehensive Copying Not Required for Uploading | Accelerating Future - Michael Anissimov has a sensible response to PZ Myer's panning of my brain emulation whitepaper. I don't think I have much to add.

I think the core question is a matter of intuitions of scale and progress: if technology X requires a humongous amount of computations/devices/research/whatever, is that an argument for regarding it as abject nonsense? In some cases one can make a clear case it does (certain computations are not doable with the resources in the universe), in others it doesn't (storing a record of all citizens, the entire human genome or all webpages are all quite doable, yet at some earlier point likely looked entirely implausible). Often there is disagreement: people I respect regard the idea of taking apart planets and converting them into technology as total silliness, yet other people I respect think that it will eventually become feasible.

Normally we estimate the scale of work needed to do something, compare that to the available resources, and make a judgement of whether it is easily doable or not. This fails for future projects because the scale and the amount of available resources is uncertain. Worse, the resources may change over time. The standard example is computing resources, where fast growth makes previously infeasible activities doable (consider how statistical language translation has evolved, or the current spread of face recognition). New algorithmic insights might make resources even cheaper (consider the jump from an O(N^2) to O(N log N) algorithm). But the same is true for many material resources: getting large amounts of paper, books or rice grains is doable on a budget today while just a few decades ago it would have been very expensive.

The obvious rejoinder to scepticism about the feasibility of something is to plot the relevant growth curve, extrapolate it and see when it crosses the line where the project becomes feasible. Doing it extra carefully, you might add plausible uncertainties in the growth and the resources needed, getting a probability distribution for feasibility dates.

But that still hinges on the lack of system-changing insights or changes: cryptanalysis can bring the date of cracking an encryption system into the present from a previously safely astronomically remote future. The discovery that the goal is not worth it or cannot be done in this way dissolves the whole issue. Trends and distributions of resources/demands work well when we are unlikely to have these crucial consideration discoveries. In domains dominated by progress through discrete insights rather than gradual refinement or growth predictability is low.

So:

• First, most people are bad at extrapolating into the future in any way. They will also have a very weak sense of the orders of magnitude involved, and underestimate the power of exponential growth. They will hence often assume that if something cannot be done at all today it can never be done.

• Second, enthusiasts tend to assume there are not going to be any discoveries blocking things. Pessimists tend to assume there will be. Both then pick evidence to support their views, with the pessimists having the winning "but you can never plan for unknown unknowns!" (However, that goes the other way around too: there might be big simplifications around the corner - maybe P=NP or brains are really simple).

• Third, discussions hence become more dominated by people's prior intuitions about the domain. People who think they understand an important sub-domain better than the original claimant tend to overestimate their ability to estimate overall feasibility.

• Fourth, trend extrapolations is nice because you can at least attempt to include empirical data, but the reliability is not great. Looking at core principles that can prove or disprove things is much better. But as the previous points argue, they have to be actual core principles rather than just good-sounding arguments: arguments tend to be biased and people overconfident in their strength.
  

Here is my suggestion for what uploading sceptics should do: demonstrate the absence of scale separation in the brain. If all levels are actually dependent on lower levels for their computational functions, then no brain emulation can be done. But it is not enough to just say this is the case, you need to show it (using, presumably, methods from statistical mechanics, systems biology and other disciplines). Regardless of the answer it is a useful project.