August 10, 2012
There is an ill wind that blows no minds
Time to apply math to important problems: the acoustics of flatulence.
It all started when I came across the light-hearted article "The mysterious forces of flatulence" which discusses the pressing question about whether flatulence could possibly propel a person. It also analyses the sound, reaching the conclusion that the characteristic frequency should be in the ultrasonic range. As the article noted, this is obviously not the case (despite occasional expressions like "he is so uptight that when he farts the dogs howl"). The post suggests that dynamical aperture cross section changes play a role - let's analyse it!
The anal sphincter can be viewed as an elastic toroid or cylinder. This is actually how it is modeled in biomechanics, see for instance the review Modelling the biomechanics and control of sphincters by Heldoorn, Van Leeuwen and Jan Vanderschoot, The Journal of Experimental Biology 204, 4013–4022 (2001). (No, the researchers are not as frivolous as me - understanding sphincter muscles is important for making prosthetics, treating various conditions and for biomimetic systems - just consider how powerful and versatile valves they are in the body!)
The simplest models are based on the three-element Hill muscle model where there are components representing the contractile, connective and dampening parts of the tissue.
Empirical data can be found in C.P. Gibbons, E.A. Trowbridge, J.J. Bannister, N.W. Read, The mechanics of the anal sphincter complex, Journal of Biomechanics, Volume 21, Issue 7, 1988, Pages 601–604 which shows that the circumferential force is to a good approximation linear in dilation. The paper also shows the importance of the anal lining for maintaining continence: there are some nontrivial engineering constraints here.
OK, let's (over)simplify things.
The tension in the muscle determines its diameter, and resists (if the diameter is small enough) anything passing through. However, pressurized contents will also force the muscle to expand.
The sphincter force will be F_s = k*d+F0 where k is a spring constant, d is the diameter and F0 is the force when the muscle is at "rest" and closed (actually a combination of background muscle tonus and the above lining mechanics).
We can model the diameter as a dampened oscillator:
m d'' + mu*d' + k*d + (F_c - F_0) = 0
where m is the mass, mu is a dampening constant, F_c is the pressure from the contents. We also decree that if d<0 it is just set to 0 - at this point incompressible properties of the tissue come into play.
What should F_c be? Clearly it depends on the internal pressure, but there might be a dependency on d too. Let's start with the simple case.
If the pressure is constant the above equation has two types of solutions:
If F_0 > F_c, d=0 is clearly an attractor: the sphincter stays closed.
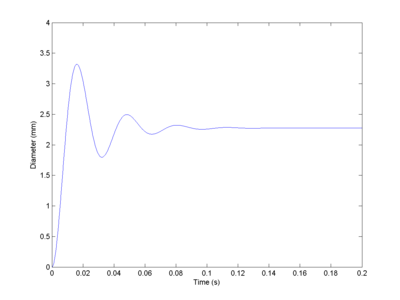
If F_c > F_0 then there will be a d>0 fixed point at d=(F_c-F_0)/k. If mu < 2 sqrt(mk) there is under-damping and the approach to this point will be oscillatory with frequency sqrt(k/m-mu^2/4m^2).
Making the crude assumption that m is on the order of a few grams, k is around a few hundred N/cm (say 300) and dampening might be about 1 Ns/m. Then I get a frequency of 166 Hz. Not too implausible. Or in any case, not in the ultrasound range.
Note that this oscillation will decay over time in this simple model. But the flow of gas could help maintain it: as the aperture narrows the pressure increases, doing work to expand the aperture and hence injecting energy into the system. So the tone can be maintained for a long time.
Still, this model only explains the high frequency pure tone sounds. It does not explain the "whoopee-cushion" sound, which clearly has a far lower frequency. Getting down there either requires a suspiciously low k or another mechanism.
An obvious extension is that the gas pressure is not constant and that we have relaxation oscillations.
The theory of orifice plates is clearly applicable. Fortunately we do not have to deal with choked flows (since they represent supersonic speeds, which the original blog post shows are unlikely). The volume flow rate through a circular orifice of diameter d is
Q = C_d pi d^2/4 sqrt(2 DeltaP/rho)
where C_d is the discharge coefficient (0.61 for a flat plate orifice, 1 for a short tube), DeltaP the pressure difference in Pascals and rho the gas density.
Modelling the pressure and density seems to be a bit complicated; one can model the rectum as a balloon where the pressure depends on radius and wall tension. (Real balloons and organs have fairly complicated inflation behaviour with stiffness and hysteresis, see for example W. A. Osborne and W. Sutherland, The Elasticity of Rubber Balloons and Hollow Viscera, Proceedings of the Royal Society of London. Series B, Containing Papers of a Biological Character Vol. 81, No. 551 (Nov. 23, 1909), pp. 485-499). Using the ideal gas law it is possible to link pressure and density and model their change as gas is let out. However, things get rather nonlinear.
I decided to use a far simpler model where the pressure is reduced by the flow and is restored at a constant rate:
DeltaP = -k1 Q + k2
where k1 and k2 are constants.
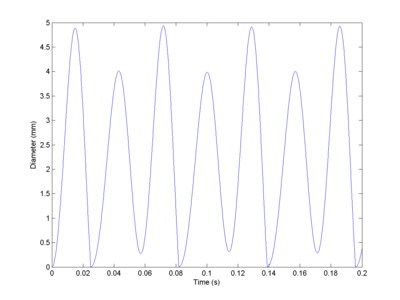
This produces relaxation oscillations. The sphincter lets out gas, the pressure declines and it closes (fast). The pressure increases, but the sphincter opens relatively slowly and the flow depends on the square diameter, so the pressure will get high enough to bring it back to the original open state.
Depending on parameters the oscillations can have multiple sizes. The most important thing is that it doesn't seem hard to get sufficiently slow oscillations to explain the low frequency noises.
Obviously, for predictive purposes (i.e. when investigating how to achieve a silent one, or to deduce bodily parameters from sampled sound spectra) a full model of rectal tension and gas density, as well as more carefully chosen material parameters should have been used. But I think this serves as a preliminary analysis of how different frequency embarrassments are produced. It is all about the eigenvalues.