March 04, 2010
The sun rises more surely with Jeffreys than Laplace
The sunrise problem is one of the perennial problems of probability and particularly relevant for the research we do at FHI: how do we estimate a probability for something we have never seen?
The "classic" solution is Laplace's rule of succession that provides us with the answer that if we have seen N sunrises, the probability for another sunrise tomorrow should be (N+1)/(N+2).
This can be calculated this way: Seeing N out of N possible occurrences of an event with true probability p has probability p^N. If we know this has happened, we have a probability distribution for p of the form (N+1)p^N, where the (N+1) terms is a normalization constant. Calculating the expectation for p we get (N+1)/(N+2).
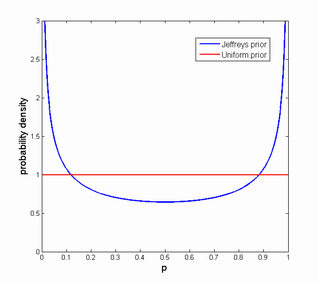
However, this assumes an uniform prior over p: each probability is equally likely (the principle of indifference). While this might seem reasonable, probabilities in the real world tend to either be very small (something almost never happens) or very large (it almost surely happens). Worse, when estimating probabilities we are often interested in order of magnitude rather than absolute values. But a uniform distribution over log p is not uniform over p.
One approach to this is to use an "un-informative" prior, a prior estimate that expresses our uncertainty but is also invariant over the transformations we might think are reasonable for the problem. In this case the Jeffreys prior seems useful. In particular, the version of it (it has a different version for different problems) we want is the one used for estimating a biased coin, J(p) = 1/sqrt(p(1-p)).
Plugging the prior into the previous analysis and using Bayes' rule we get
P(p | having seen N out of N) = (N+1)p^N J(p) / integral01 (N+1)p^N J(p) dp
Unfortunately the integral below the denominator is a messy hypergeometric function. The forms for integer N are simpler (no hypergeometrics) but still unwieldy.
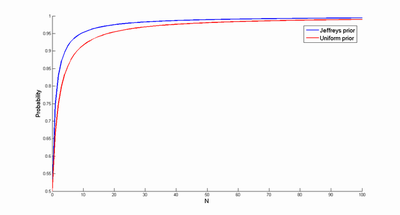
Using numeric integration instead produces the following probability estimates (care must be taken when integrating close to 0 and 1, since J(p) is badly behaved there. Whee!)
The blue curve is using the Jeffreys prior, the red Laplace. So if we believe this prior is better than the uniform one, we will be more confident that the sun will rise tomorrow. Which is a bit surprising, given that the prior actually puts much of its probability mass close to zero. But that part of the prior quickly gets "overruled" by the N observations, amplifying the effect of the other big lump of probability mass near 1.
Posted by Anders3 at March 4, 2010 11:26 AM