January 18, 2010
Bark in the bread moves the percolation threshold
How resilient is a society to disruptions? Here is one simple model with some interesting dynamics.
The society is modelled as a network of nodes, where each node gets inputs (information, energy, money, goods etc.) from other nodes. It needs several kinds of input to function, so if it cannot get all of them it will stop working. This can of course cause a cascade as more and more nodes stop working due to shortages.
If each node has k inputs, and the probability that a node is working is p, then the probability that this node has all working inputs is p^k. While the equation p=p^k only has the real solutions p=0 and p=1, discrete networks have subnetworks that can luckily avoid collapse. But they are very small compared to the whole network: this model is very unstable, and any small disruption tends to disrupt the whole system.
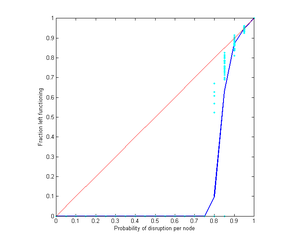
[Erratum: the x-axis has the wrong label below. It really denotes the probability p that a node is *not* disrupted.]
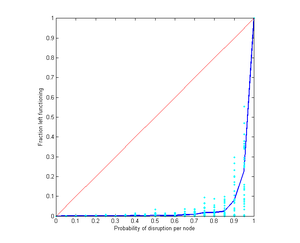
Number of stably functioning nodes when a network with k=1 starts with different fractions of failed nodes. The blue line is the average of individual runs, shown in turquoise. The red line indicates the perfect case, where taking out a certain fraction has no further effect.
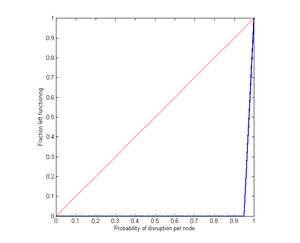
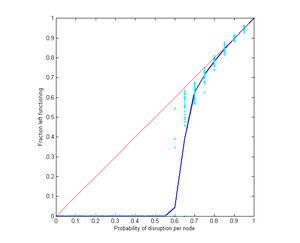
As above, but each node now requires two goods. Even a very small disruption crashes all nodes.
Substitutes
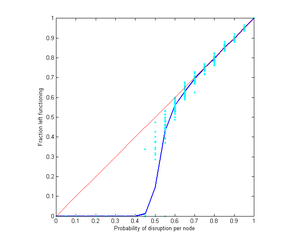
In real societies different goods can substitute for each other. If there is a shortage consumption shifts to an alternative, until all the alternatives are unavailable. This softens the effect of multiple dependence.
Here are the results of simulating a network with 1000 nodes and different numbers of available substitutes.
One possible substitute:
Two possible substitutes:
Three possible substitutes:
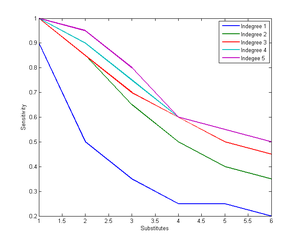
Here is a diagram of sensitivity as a function of number of substitutes and number of inputs:
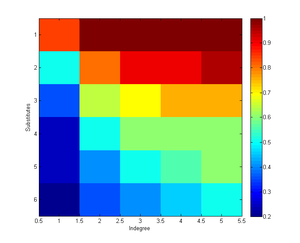
The colours denote the lowest disruption probability where just a fraction of 0.05 of nodes remain active; warm colours indicate sensitive societies (crash at high p). When there are no substitutes sensitivity is very high. Substitutes rather efficiently counteract the effect of multiple dependencies.
Allowing nodes to have a uniformly distributed in-degree or number of substitutes does not change the outcome much. They were equivalent to a somewhat reduced in-degree or number of substitutes respectively. Even making certain nodes more likely to be the default source of different goods (i.e. node i links to node 1 to i-1) did not have much effect since substitution could circumvent such bottlenecks. Making the substitute goods equally skewed surprisingly did not worsen the situation much, and instead tended to soften the percolation transition.
One conclusion seems to be that if we want to increase the resiliency of our society we should work on increasing substitutability. Devices and software should be able to use alternative infrastructures. Knowledge of what can be substituted for what should be disseminated (so no time is lost when disaster strikes in trying to figure it out). This is particularly true in areas where many different kinds of inputs are needed.