September 22, 2008
Bayes, Moravec and the LHC: Quantum Suicide, Subjective Probability and Conspiracies
The recent transformer trouble at the LHC has got many commenters to remember the somewhat playful scenario in Hans Moravec's Mind Children (1988): a new accelerator is about to be tested when it suffers a fault (a capacitor blows, say). After fixing it, another fault (a power outage) stops the testing. Then a third fault, completely independent of the others. Every time it is about to turn on something happens that prevents it from being used. Eventually some scientists realize that sufficiently high energy collisions would produce a vacuum collapse, destroying the universe. Hence the only observable outcome of the experiment occurs when the accelerator fails, all other branches in the many-worlds universe are now empty. (This then leads up to a fun discussion on quantum suicide computation)
As Eliezer and other bright people realize, one transformer breaking before even the main experiments is not much evidence. But how much evidence (in the form of accidents stopping big accelerators) would it take to buy the anthropic explanation above?
Here is a quick Bayesian argument: Let D be that the accelerator is dangerous, N be that N accidents have happened so far.
P(D|N) = P(N|D)P(D)/P(N) =P(N|D)P(D)/ [P(N|D)P(D) + P(N|-D)P(-D) ]
Since P(N|D)=1 by assumption we get
P(D|N)=P(D)/ [P(D) + P(N|-D)(1-P(D)) ]
Let X=P(D) be our prior probability that high energy physics is risky in this way, and Y=P(1|-D) be the probability that one accident happen in the non-dangerous case. We also assume the accidents are uncorrelated, so P(N|-D)=Y^N. Then we get
P(D|N)=X/ [X + (1-X) Y^N ]
Below is a plot for N=1 and another one for N=10:
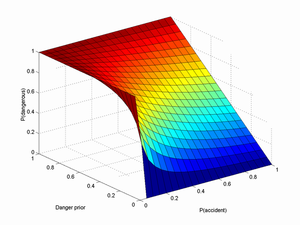
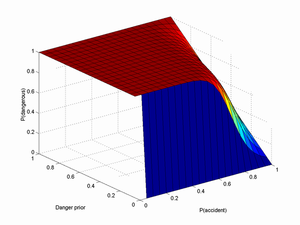
I think Y can safely be assumed to be pretty big, perhaps ~1/2 or even more. X depends on your general faith in past theoretical papers showing the safety of accelerators. In particular, I think Hut, P. and M. J. Rees (1983). "How Stable Is Our Vacuum." Nature 302(5908): 508-509 makes a very solid argument against vacuum decay (especially when combined with Tegmark, M. and N. Bostrom (2005). "Is a doomsday catastrophe likely?" Nature 438(7069): 754-754), so X < 10-9.
Plugging in N=1,X=10-9 and Y=0.5 gives us P(D|N)=2*10-9. Wow! A doubling of the estimate, all because of a transformer. Claiming the closure of the SSC is another datapoint would bring up the chance to 4 chances in a billion.
In fact, I think this is a gross overestimate because the X above is the risk per year; we didn't even get one second of collisions. If the risk is actually on the order of one disaster per year, we should expect to run the accelerator for about half a year before something happens preventing the collision. If the risk is much higher, then we should expect an earlier shut-down. So given that we got one or two early shut-downs, we should (if we believe they were due to branch-pruning) think the risk is much higher, say about 31 million times higher (number of seconds in a year) or more. But if we were to live in such a dangerous universe where every TeV interaction had a decent chance of destroying its future lightcone, then the Tegmark and Bostrom argument suggests that we are in a really unusual position. So getting a consistent and likely situation is hard if you think disaster is likely.
So, how many accidents would be needed to make me think there was something to the disaster possibility? Using the above estimates, I find P(D|20)=0.001 and and P(D|30)=0.52. So if about 30 uncorrelated, random major events in turn prevent starting the LHC, I would have cause to start thinking there was something to the risk.
However, the likelihood of some prankster or anti-LHC conspiracy trying to trip me or the LHC people up seems to be larger than one chance in a billion per year. This would add an extra term to the equation, giving us P(D|N)=X/ [X + (1-X) (Y^N + Z) ] where Z is the probability of foul play. Adding just one chance in a billion reduces the P(D|30) estimate to 0.34, which is still pretty big. If it is one chance in 100 million it becomes 0.08, and one chance in 10 million gives 0.01. However, I think the chance for the existence of a conspiracy able to successfully cause 30 LHC shutdowns in a row (without anybody finding any evidence) is hardly on the order of one in 10 million.
In the unlikely case we actually get a high P(D) estimate, it might seem we have got a way of doing quantum suicide computing (connect it to a computer trying random solutions, destroy the universe if the wrong one is found, reap benefits in all remaining universes) or even terrorism prevention (automatically destroy all universes where terrorist attacks occur, to the surviving observers it will look like terrorism magically has ceased). Unfortunately Y is likely pretty big. We should hence expect to see a lot of universes where the LHC simply fails because of the usual engineering problems, and leaves us with the wrong solution or the aftermath of terrorism. Quantum suicide computing/omnipotence requires absurdly reliable equipment.
Posted by Anders3 at September 22, 2008 06:39 PM