February 05, 2008
The Julia-Mandelbrot Set
The Mandelbrot set is defined as those complex number c where the sequence zn+1=zn2+c, starting with z0=0, does not diverge to infinity. The Julia set for a complex number c is defined as the starting points z0 where the sequence does not diverge. Both are kind of dual to each other, and at least the Mandelbrot set often looks locally just like corresponding Julia sets.
Another way of viewing this is to join them into a four-dimensional set inhabiting C2: the set of points that for a given c and z0 do not diverge. Here are some crude images of sections through it:
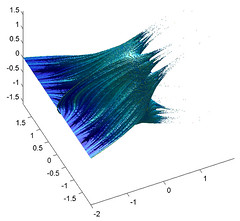
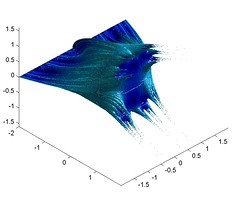
These are sections in the imag(c)=0 hyperplane. They can be viewed as stacks of Julia sets along the real line, ranging from the line set at c=-2 over the San Marco fractal and unit circle to the c=1/4 blanchemange, which implodes to Fatou dust - in this picture the long feelers extending in the positive c direction. Note the neat parabola touching the c=-2 line.
If we move to the imag(c)=0.4 hyperplane we get more twisting, and the c=-2 line dissolves into dust-tendrils. The overall shape remains, but as the hyperplane moves towards increasing imaginary levels the whole thing twists into ever thinner dust.
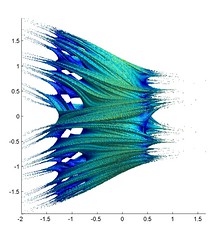
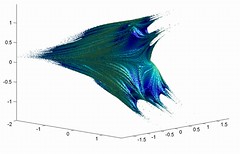
Looking from the perspective of changing z0 rather than c, we get the following shapes:
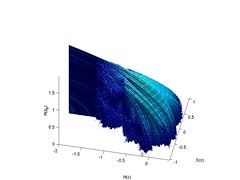
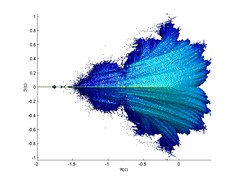
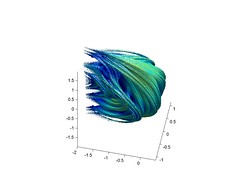
The "equator" is the Mandelbrot set, and as z0 changes it warps in different ways. The last picture shows a plane with imag(z0)=0.4.
It is possible to plot the intersection between the set and random hyperplanes too, revealing a bit of its "generic" appearance:
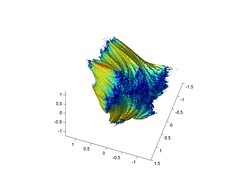
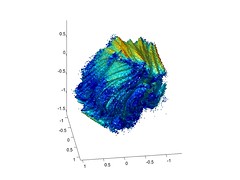
I made this using Matlab, plotting isosurfaces of convergence vs. nonconvergence. Very non-optimized code, slow plotting and produces plenty of artefacts, but a quick hack. Properly it should be raytraced or at least run as a z-buffer rendering. The color denotes the smallest magnitude an iterate achieved .
Posted by Anders3 at February 5, 2008 01:41 PM