Andart

Universal Equations

Here is a cool result: for any continuous function f(x) there is a solution y(x) of the equation y''''y'²-3y'''y''y'+2(1-n^-2)y''³=0 so that |f(x)-y(x)| < epsilon(x), where epsilon is any positive continuous function. That is, there is a solution that approximates nearly any function you care to name arbitrarily well.

This is from the paper Another universal differential equation by Keith Briggs. It is a simpler version of Rubel's universal differential equation.

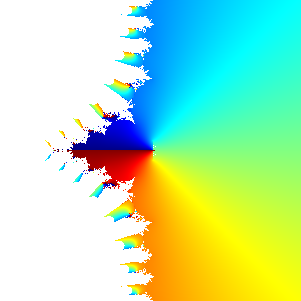
This reminds me of another cool result. Voronin showed that the Riemann zeta function is universal in the sense that for any complex analytic function that has no zero in a disk of radius 1/4 around the origin, there is a piece of the zeta function along the line Re(z)=3/4 that is closer to it than epsilon, for any epsilon. This in turn implies that it is a fractal in a sense (since it approximates small pieces of itself), that it is a catalog of all smooth continuous line drawings, and that any text is represented in Morse code somewhere in the zeta function domain.

I think this implies that the Mandelbrot-like set in the picture (which is the Mandelbrot set for the zeta function) ought to contain nearly any other Mandelbrot-like set. So while the usual Mandelbrot set does not contain the cubic Mandelbrot, this one ought to contain both since in small regions we get local dynamics that looks exactly like z^2+c and z^3+c. Finding them is another matter entirely.

Posted by Anders3 at December 24, 2007 08:44 PM