Andart

When is it Rational to Get a Technology?

A discussion on the Swedish transhumanist mailing list Omega got me thinking about this problem: when is it rational to start using a new technology? If you buy it as soon as it arrives you have no information on whether it is worth it, but waiting for a long time means you might miss something good.

In practice we rely on advice and reports from others - but they are unreliable evaluators. However, Bayes' theorem is more powerful:

Assume the true value of the technology to me is an outcome x of a stochastic variable X, with probability density function f(x). People give evaluations y_i = x + epsilon, where epsilon are i.i.d distributed by g(epsilon). When there are N evaluations we can calculate

P(X=x|{y_i}) = P({y_i}|X=x)P(X=x)/P({y_i})

The divisor is independent of x, so it will not matter for our evaluation. We can move it into a normalisation constant C. The independence of the y's gives us

P(X=x|{y_i}) = C P(X=x) Π_iP(y_i|X=x)

Let us assume f and g are both normally distributed with variance σ₁² and σ₂² respectively, and zero means. Then the above equation turns into

P(X=x|{y_i}) = C e^-x2/2σ₁2Π_ie^{-(y_i-x)2/2σ₂2}= C e^{-x2/2σ₁2 -Σ_i(y_i-x)2/2σ₂2}

which is another normal distribution with mean μ = ∑_iy_i/(N+σ₂²/σ₁²).

Now we can evaluate the expected value of x based on the observations and see if it is positive enough. However, we want a robust estimate of whether it is worthwhile to get the technology or not. But since we know the posterior distribution we can calculate a 95% confidence interval. We know the "true" value will be inside this interval, and once the entire interval is above a certain limit we get the technology.

Of course, we do not really know σ₂², but calculating the standard deviation of the y's works decently. We can assume we know σ₁² (and that f(x) is normal) by experience. In practice changing σ₁² doesn't have an enormous effect beyond making our estimates more or less conservative.

Here is a simulation. The green line represents the true value of x, the grey dots represent evaluations arriving over time (both assumed to have variance 1 and zero means). The red line is the decision boundary (is the technology positive or not?) and the blue lines are confidence intervals.

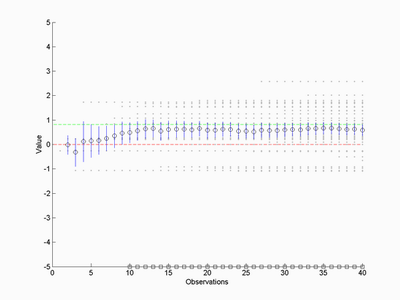
The squares mark times when the confidence interval is completely above the decision boundary, i.e. there is just 5% chance that x is negative. In this case it would be sensible to get the gadget at time 10.

How reliable is this kind of estimate? Sometimes I get isolated 'go'-signals as the early estimates jump around, and occasionally false positives happen. Overall it seems to be pretyt robust, with indeed errors happening less than 5% of the time. One can play safe of course by making sure the interval is above the decision boundary two or more consecutive timesteps to insure there are no flukes.

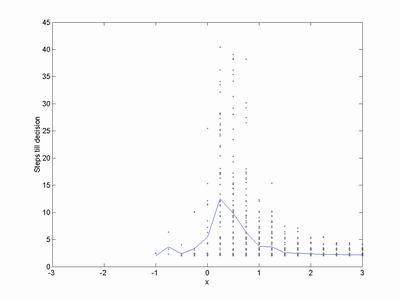
The time it takes to reach a decision is surprisingly short. For very good gadgets (x>2) the average time is about 2-3 steps. It becomes harder to choose close to neutrality, where convergence may take many tens of steps. Still, even here it is not uncommon for rapid decisions to happen. Erroneous decisions (for negative x) also happen quickly: these are driven by the estimates jumping around randomly at the start, accidentally ending up on the wrong side of the decision boundary.

So the conclusion is: if a few of your friends are very enthusiastic (i.e. beyond twice their normal standard deviation) then it is a good chance that the new gadget is worthwhile. Otherwise, wait until you get much more people to weigh in.

In reality, things are likely not normally distributed but have some skew distribution, and people are clearly not independent in their judgements. Skew distributions are relatively easy to add to this framework while dependent estimates would require more footwork. But all in all, you don't seem to need an enormous crowd to get some wisdom out of it.

Posted by Anders3 at August 5, 2007 12:45 PM