Andart

Cubic Terms Make Smart People Bankrupt

I recently came across the paper Do you have to be smart to be rich? The impact of IQ on wealth, income and financial distress by J L Zagorsky (Intelligence, in press). The subject is interesting: does higher intelligence increase income and saved wealth, and does it protect from making bad financial decisions? Zagorsky reaches the counterintuitive conclusion that it does not improve overall wealth despite increasing income (the income part was known before), and that there is a nonlinear relationship between IQ and being in financial distress: being smarter does not reliably make you economically wiser.

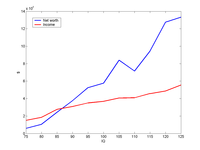
Data from table 2, showing median income and net worth. The medians are at least increasing!

These conclusions would have been good if they had not been marred by "machine thinking". There was frequent references to which piece of software that was being used, as if this would be relevant when the statistical methods were stated. A number of regressions were done using multiple methods, for the stated purpose of dealing with the skewedness of financial data. But if financial data are too skew, wouldn't log data work better? I got the impression of the author simply using the entire toolbox because it was there. Using several different kinds of regressions doesn't give much information to compare with and increases the chances of spurious significance. A better approach might be something along the lines of Sala-I-Martin's "millions of regressions" method where the distribution of coefficients of a particular variable is analysed when different sets are included in the regression. This gets around the risk of handpicking explanatory variables.

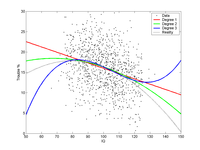
The most irritating case was the financial distress analysis where a third degree polynomial was fitted because: "First, by using Excel's chart trend-line function, a polynomial of order 3 visually best fits the data series shown in Table 5." Here is the data, I leave it to the viewer to determine whether this really looks like a third degree curve:

"Second, a common way of ranking competing logistic models is comparing their Akaike's information criteria (AIC) (Akaike, 1974). The model with the smallest AIC fits the data best. Starting from a linear model the AIC falls until IQ cubed is added, but then it rises sharply once IQ raised to the fourth power is included." Here the author does not explain how AIC was applied, but given the skewness of financial data that does not appear to be controlled, one cannot assume normal errors and that may quite possibly give skewed results too if the software assumes normality.

The resulting conclusion that high IQ people may be more likely to suffer financial trouble seems to be due to the cubic term. Zagorsky tries a number of explanations:

"One explanation is that higher IQ score individuals might
be busier and less focused on routines like paying bills. Another explanation is those with a higher IQ score might lead a life-style that is closer to the financial precipice because they feel they are smart enough to calculate and understand all relevant factors. A third explanation is that smarter people have a better memory and are more likely to remember mistakes."

There is probably some truth to this. But a far simpler explanation is that it is a case of overfitting.

A fitted high degree polynomial will rush towards (positive or negative) infinity outside the interval of points it has been fitted to. The financial data seems to be mostly in the interval 75-125 (as would be expected from a normal population) but is extrapolated up to 140 in table 7. No wonder the risks start increasing!

Here is a toy example, where I simulated 1000 individuals with IQs 75-125, with a trouble probability that was a simple parabolic curve plus noise. I fitted a linear, quadratic and cubic curve to them.

The blue cubic curve suffers from clear overfitting. Zagorsky's regression is admittedly different, but the evidence for a need of third degree polynomials does not look that strong.

In the end, this paper is a good example of why we should not let our software do our scientific thinking. Research is not just about getting a dataset, plugging it into a statistical model and coming up with an explanation of why the result is plausible.

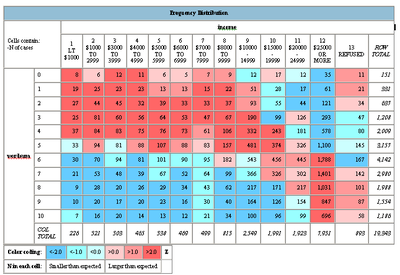
Still, what is not enough for a scientific paper may be enough for a blog. I took the WORDSUM data from the GSS as a proxy for intelligence, and plotted the frequency distribution of INCOME.

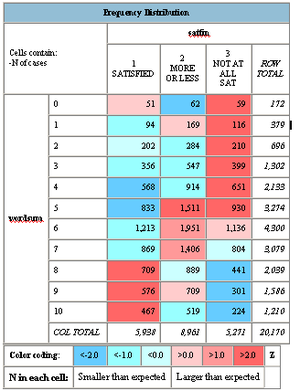
There seems to be a pretty solid link between having more than 4-5 points of WORDSUM and getting a better income. Unfortunately I did not find any variables useful to estimate savings, so we cannot check the most interesting issue in Zagorsky's paper. Plotting whether people feel they are satisfied with their financial situation showed a clear trend:

Being above average seems to make you more satisfied. maybe this is just because of the higher income, but I would suspect savings do play a role.

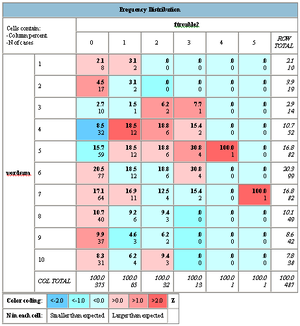
There are variables representing economic trouble, and when summed together and plotted with WORDSUM we get this:

Not much evidence for more trouble at the high end, but it looks like some more financial distress in the lower mid part of the intelligence gaussian. This is where there are enough people to get some data, they have reasonably large incomes, and they might be stupid from time to time. There is also a pretty strong anticorrelation (-0.38) between WORDSUM and thinking that there is no point in planning, that one has little control over bad events and good events are mostly luck (I added BADBRKS, LITCNTRL, MOSTLUCK, NOPLAN). That kind of fatalism and external locus of control seems pretty likely to predispose to financial troubles and low saving.

Posted by Anders3 at April 9, 2007 02:02 PM