March 11, 2007
Crocus Fractals


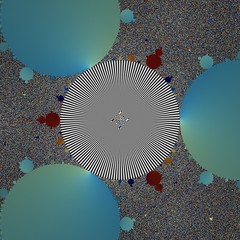
During a boring lecture I came up with this fractal; it is based on iterating f(z)=cz/(1+z^3) where c is close to the unit circle. Going just outside the unit circle produces a less dramatic effect:


What is really going on here? These fractals are essentially the Julia sets of f(z), so looking at their corresponding Mandelbrot set can be revealing. If we start with a critical point z0 of f(z) (i.e. f'(z0)=0) and iterate it for different choices of c, we get the following picture:
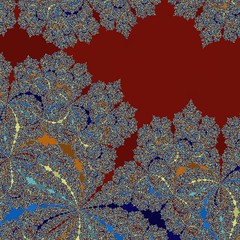
The central disc is limited by the unit circle. Inside the Julias are boring Fatou dust since the map is so contractive that the images of the zeros and poles don't get to expand much. The three big regular domains represent areas where the Julias are similar to the standard Julia set of Newton's method applied to z3-1. As we move outwards the topology becomes more fun; the big discs are surrounded by circular buds containing 3*2n cycles, making the Julia sets consist of border points where the basins of the three attractor points meet from multiple directions in each point. Conversely, the buds on the unit circle contain other periodic cycles.
The chaotic zone represents the area where most or all of the complex plane is chaotic: the Julia set is dense. As c moves across the edge from one of the ordered buds the spines extend and twist, forming beautiful spirals that slowly fill everything. And inside the chaos of the c-plane, of course we get small classic Mandelbrot sets whenever the dynamics happen to look like a quadratic map. I was a bit surprised not to get any of the "Mandelbrot's cat" set corresponding to cubic dynamics given the cubic term in f(z). I think, but cannot prove, that there are filiaments linking the Mandelbrots to each other through the chaos. There is certainly a ray along the negative real axis.
Posted by Anders3 at March 11, 2007 09:12 PM