January 03, 2007
Letter substitution graphs and percolation theory
An old game is to take a word and substitute one letter to make a new word, and then continue until you end up with something completely different (i.e. from 'old' to 'new'). I remember reading about it in Scientific American many years ago, and it may originate with Lewis Carrol although he allowed insertions, deletions and permutations. It becomes more manageable if only substitutions are used, since then just words of the same length are possible to transform into each other.
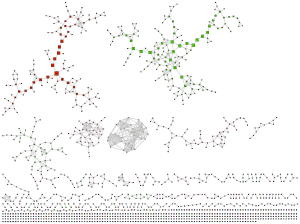
Recently I was asked to look into the network properties of Lojban gismus (why? for secret and mysterious reasons, of course :-). I wrote a little program to check 1-letter substitutions and if they resulted in another valid word a link was added between them. The resulting graph can be found here as PDF.
It fits with the earlier description, a number of disjoint subgraphs ranging from a few very large one to an archipelago of isolated words. An interesting feature is that while most parts of the network are tree-like, some are much more densely connected. Is this a normal feature of languages, or an artifact of Lojban's artificiality?
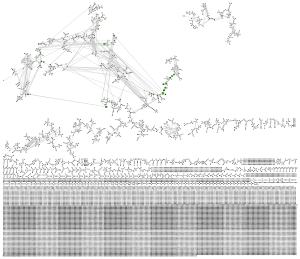
I tried it on English. Using SCOWL 6 with British spelling and words on lists up to 70, I put together graphs for 2-letter, 3-letter, 4-letter, 5-letter and 6-letter words. In these cases the graphs are above the percolation threshold and densely connected with only a few tree-like parts and unlinked clusters.
In general, if we have an alphabet of size A and look at length N words, the space of possible words is AN large and each word has just (A-1)N neighbours. Hence the fraction of neighbours declines nearly exponentially. The number of W(N) real words looks like a Poisson distribution with a peak around N=8 for English.
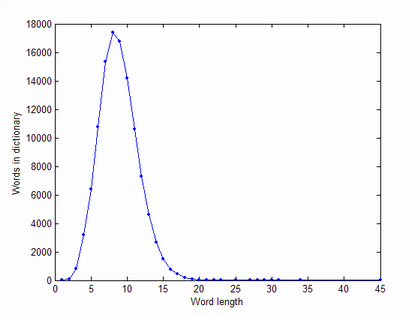
The chance that a given word has at least one neighbour is, assuming independent probabilities, P(N)=1-(1-rho(N))(A-1)N where rho(N)=W(N)/AN is the density of words. The result is a pretty rapid decline for increasing N, that soon crosses the percolation threshold 1/W(N):
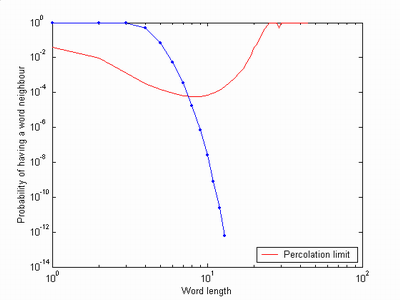
We should see a breakup of the clusters between length 7 and length 8 words, which also happens.
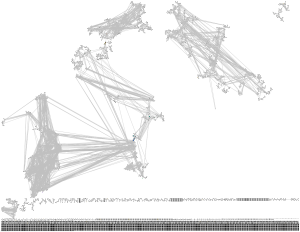
The giant component for length 7 words looks a bit fragile and has lost a sizeable cluster, and at length 8 it has turned into a cloud of clusters:
Beyond, the graphs become even more disjointed; among length 10 words the largest cluster is just 24 words large (fittingly enough, it is the words that can be reached from 'clustering') and most "clusters" are one or two words.
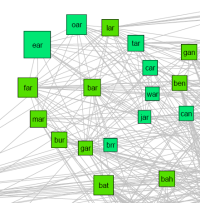
Since Lojban has a much smaller lexicon (about 8000 according to Langmaker) it may not be surprising that even the root words form a cloud of clusters. The distribution and individual graphs also looks a bit like the length 8 graph. The inhomogenities seen in both are likely due to the pecularities caused by phonology, making some letters likelier alternatives to each other because they correspond to similar sounds. As Lojban grows I expect it to reach percolation in a few hundred to a thousand more words, unless pecularities of design prevent it.
As an aside, I feel inordinately proud to find my warning sign in lojban!
Posted by Anders3 at January 3, 2007 02:35 PM